Clustering in NCSS
NCSS contains several tools for clustering, including K-Means clustering, fuzzy clustering, and medoid partitioning. Each procedure is easy to use and is validated for accuracy. Use the links below to jump to a clustering topic. To see how these tools can benefit you, we recommend you download and install the free trial of NCSS. Jump to:- Introduction
- Technical Details
- Hierarchical Clustering / Dendrograms
- K-Means Clustering
- Medoid Partitioning
- Fuzzy Clustering
- Regression Clustering
Introduction
Clustering or cluster analysis is the process of grouping individuals or items with similar characteristics or similar variable measurements. Various algorithms and visualizations are available in NCSS to aid in the clustering process.Technical Details
This page provides a general overview of the tools that are available in NCSS for a cluster statistical analysis. If you would like to examine the formulas and technical details relating to a specific NCSS procedure, click on the corresponding '[Documentation PDF]' link under each heading to load the complete procedure documentation. There you will find formulas, references, discussions, and examples or tutorials describing the procedure in detail.Hierarchical Clustering / Dendrograms
[Documentation PDF]The agglomerative hierarchical clustering algorithms available in this procedure build a cluster hierarchy that is commonly displayed as a tree diagram called a dendrogram. The algorithms begin with each object in a separate cluster. At each step, the two clusters that are most similar are joined into a single new cluster. Once fused, objects are never separated. The eight methods that are available represent eight methods of defining the similarity between clusters. The eight clustering techniques (linkage types) in this procedure are:
- Single Linkage: Also known as nearest neighbor clustering, this is one of the oldest and most famous of the hierarchical techniques. The distance between two groups is defined as the distance between their two closest members. It often yields clusters in which individuals are added sequentially to a single group.
- Complete Linkage: Also known as furthest neighbor or maximum method, this method defines the distance between two groups as the distance between their two farthest-apart members. This method usually yields clusters that are well separated and compact.
- Simple Average: Also called the weighted pair-group method, this algorithm defines the distance between groups as the average distance between each of the members, weighted so that the two groups have an equal influence on the final result.
- Centroid: Also referred to as the unweighted pair-group centroid method, this method defines the distance between two groups as the distance between their centroids (center of gravity or vector average). The method should only be used with Euclidean distances.
- Median: Also called the weighted pair-group centroid method, this defines the distance between two groups as the weighted distance between their centroids, the weight being proportional to the number of individuals in each group. The method should only be used with Euclidean distances.
- Group Average: Also called the unweighted pair-group method, this is perhaps the most widely used of all the hierarchical cluster techniques. The distance between two groups is defined as the average distance between each of their members.
- Ward’s Minimum Variance: With this method, groups are formed so that the pooled within-group sum of squares is minimized. That is, at each step, the two clusters are fused which result in the least increase in the pooled within-group sum of squares.
- Flexible Strategy: Lance and Williams suggested that a continuum could be made between single and complete linkage. The program also allows you to try various settings of these parameters which do not conform to the constraints suggested by Lance and Williams.
Example Dataset of Clustering Data
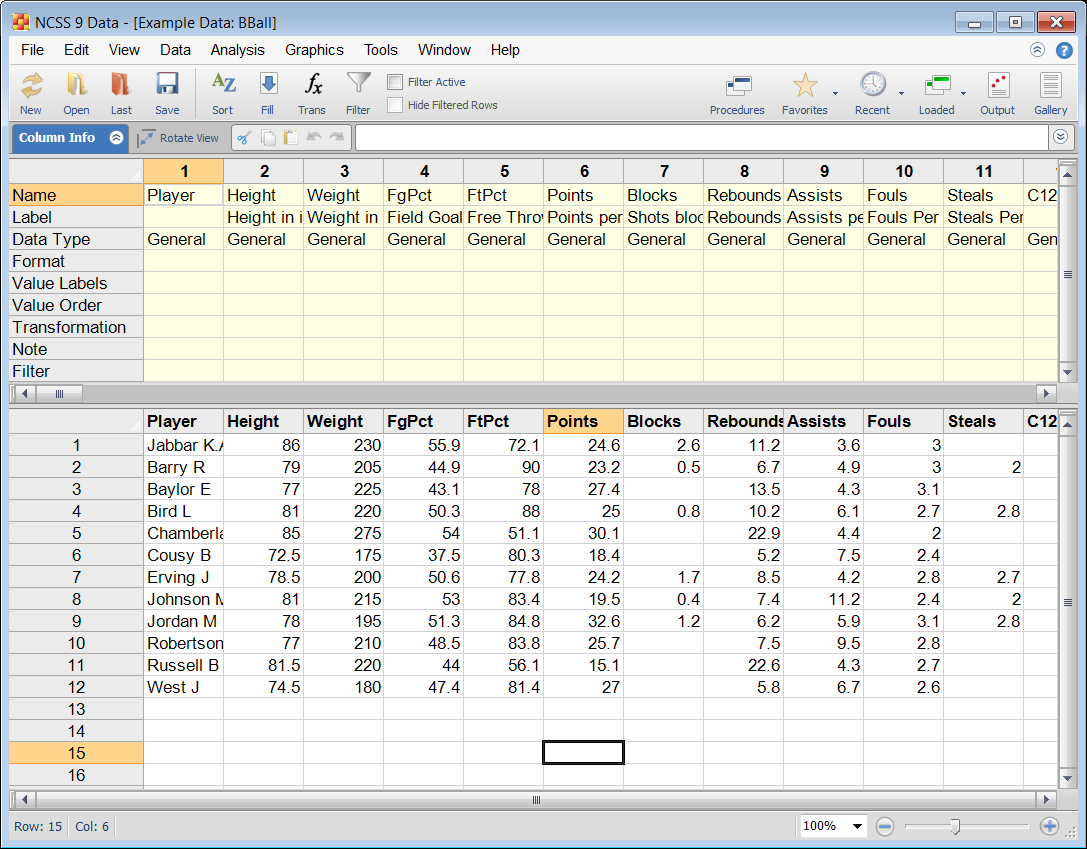
Example Setup of the Hierarchical Clustering / Dendrograms Procedure
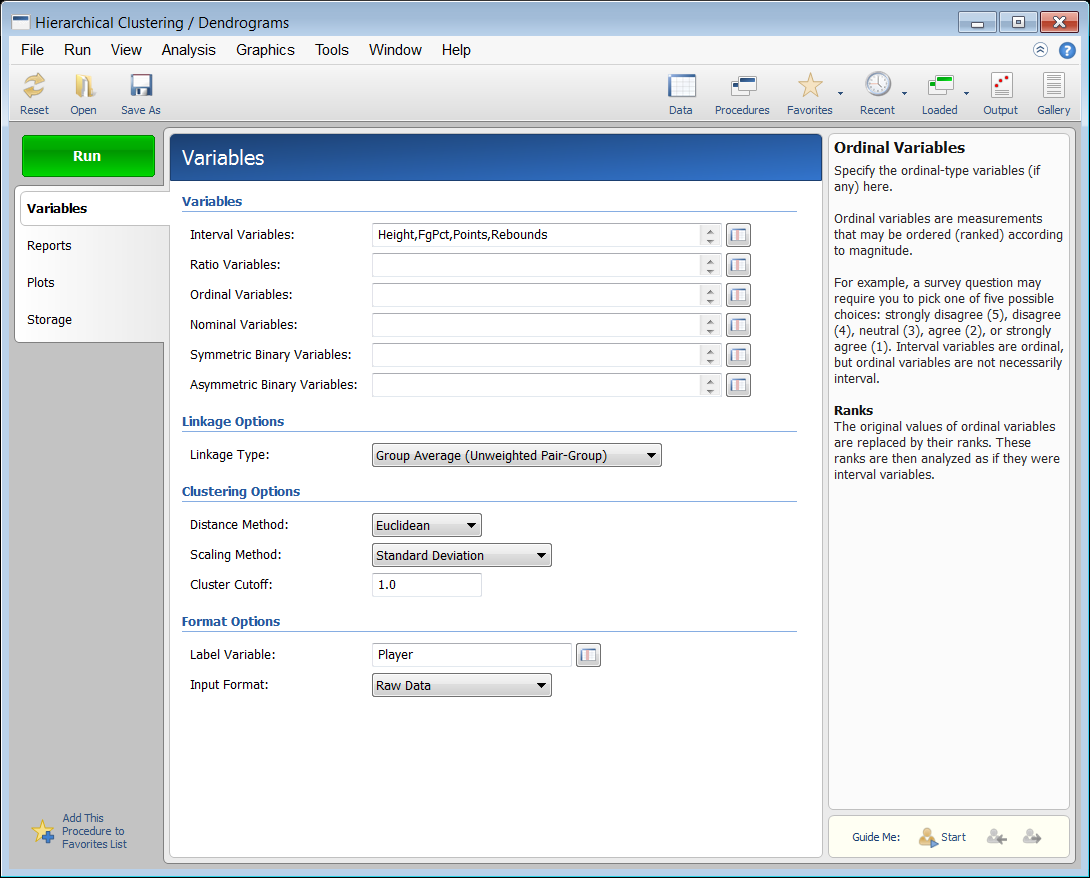
Example Output for the Hierarchical Clustering / Dendrograms Procedure
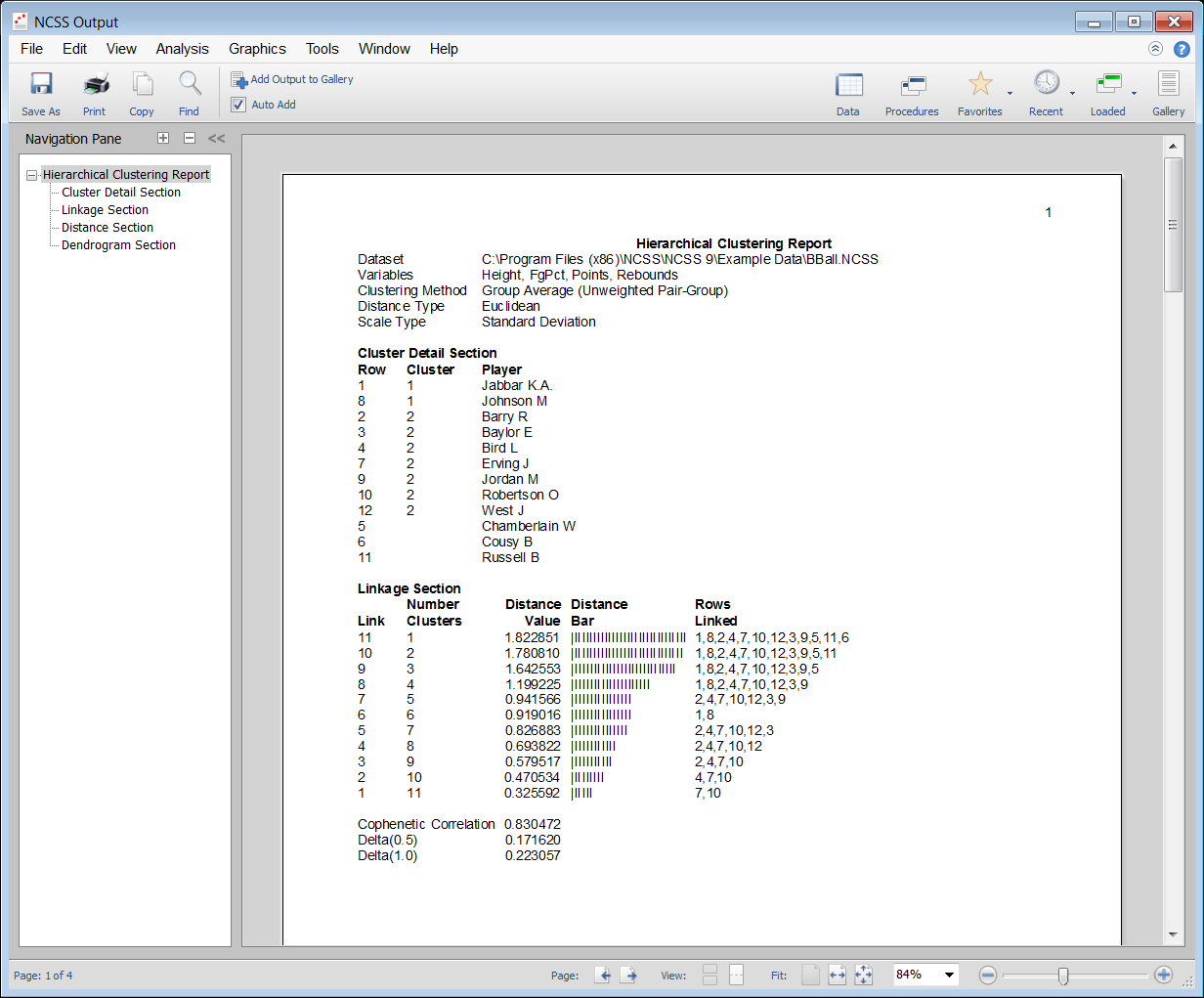
A Dendrogram from the Hierarchical Clustering / Dendrograms Procedure
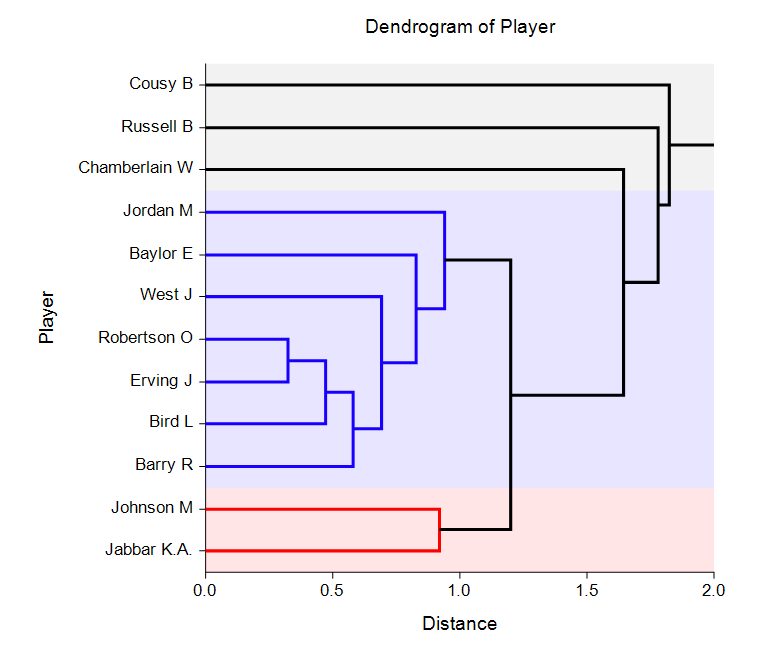
K-Means Clustering
[Documentation PDF]The k-means algorithm was developed by J.A. Hartigan and M.A. Wong of Yale University as a partitioning technique. It is most useful for forming a small number of clusters from a large number of observations. It requires variables that are continuous with no outliers. The objective of this technique is to divide N observations with P dimensions (variables) into K clusters so that the within-cluster sum of squares is minimized. Since the number of possible arrangements is enormous, it is not practical to expect the single best solution. Rather, this algorithm finds a “local” optimum. This is a solution in which no movement of an observation from one cluster to another will reduce the within-cluster sum of squares. The algorithm may be repeated several times with different starting configurations. The optimum of these cluster solutions is then selected. Some of the reports available in the this procedure include iteration details, cluster means, F-Ratios, distance sections, and bivariate plots.
Some Bivariate Plots from the K-Means Clustering Procedure
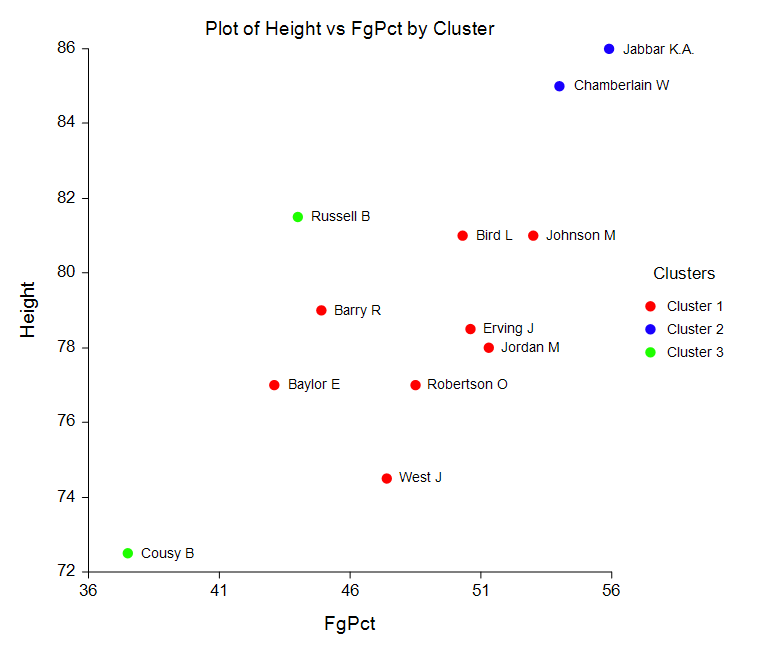
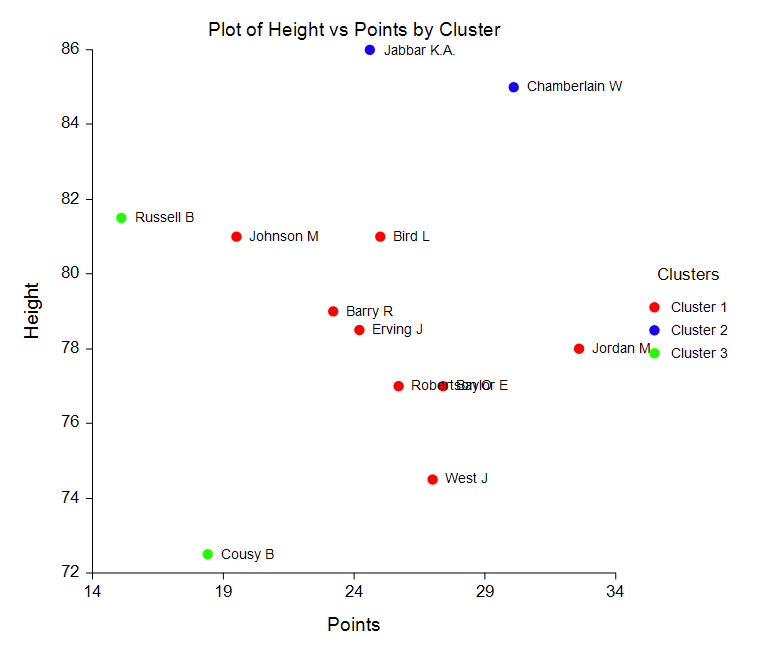
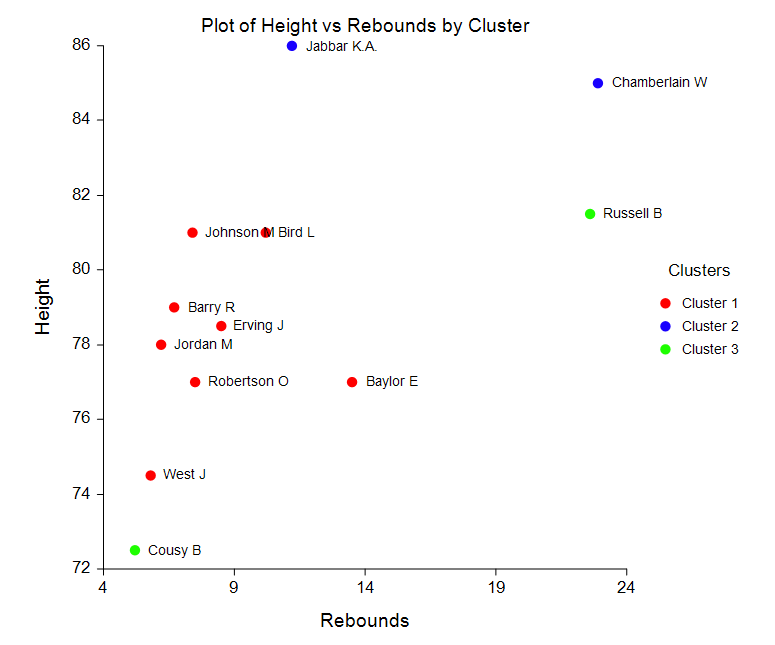
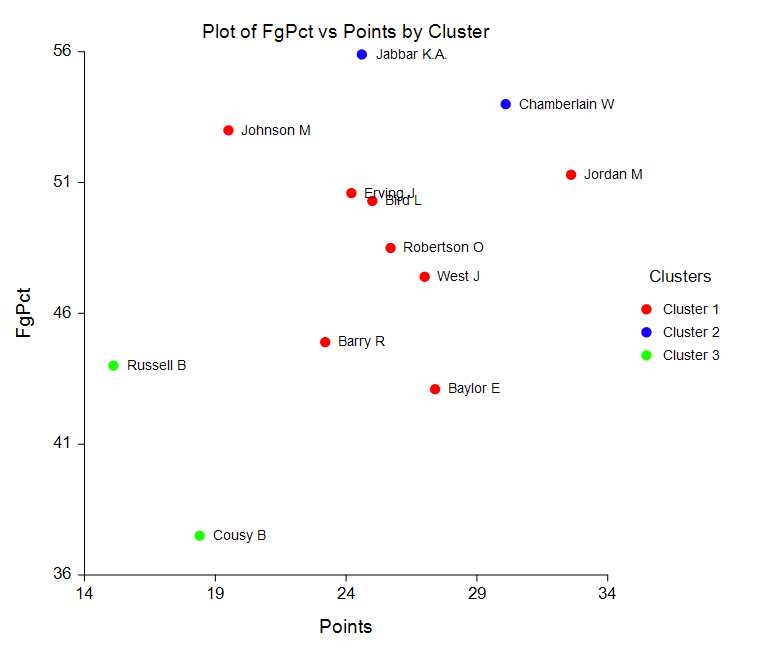
Medoid Partitioning
[Documentation PDF]The objective of cluster analysis is to partition a set of objects into two or more clusters such that objects within a cluster are similar and objects in different clusters are dissimilar. The medoid partitioning algorithms available in this procedure attempt to accomplish this by finding a set of representative objects called medoids. The medoid of a cluster is defined as that object for which the average dissimilarity to all other objects in the cluster is minimal. If k clusters are desired, k medoids are found. Once the medoids are found, the data are classified into the cluster of the nearest medoid. Two algorithms are available in this procedure to perform the clustering. The first, from Spath, uses random starting cluster configurations. The second, from Kaufman and Rousseeuw, makes special use of silhouette statistics to help determine the appropriate number of clusters.
Medoid Algorithm of Spath
This method minimizes an objective function by swapping objects from one cluster to another. Beginning at a random starting configuration, the algorithm proceeds to a local minimum by intelligently moving objects from one cluster to another. When no object moving would result in a reduction of the objective function, the procedure terminates. Unfortunately, this local minimum is not necessarily the global minimum. To overcome this limitation, the program lets you rerun the algorithm using several random starting configurations and the best solution is kept.Medoid Algorithm of Kaufman and Rousseeuw
Kaufman and Rousseeuw present a medoid algorithm which they call PAM (Partition Around Medoids). This algorithm also attempts to minimize the total distance D (formula given above) between objects within each cluster. The algorithm proceeds through two phases. In the first phase, a representative set of k objects is found. The first object selected has the shortest distance to all other objects. That is, it is in the center. An addition k-1 objects are selected one at a time in such a manner that at each step, they decrease D as much as possible. In the second phase, possible alternatives to the k objects selected in phase one are considered in an iterative manner. At each step, the algorithm searches the unselected objects for the one that if exchanged with one of the k selected objects will lower the objective function the most. The exchange is made and the step is repeated. These iterations continue until no exchanges can be found that will lower the objective function. Note that all potential swaps are considered and that the algorithm does not depend on the order of the objects on the database.Fuzzy Clustering
[Documentation PDF]Fuzzy clustering generalizes partition clustering methods (such as k-means and medoid) by allowing an individual to be partially classified into more than one cluster. In regular clustering, each individual is a member of only one cluster. Suppose we have K clusters and we define a set of variables that represent the probability that object i is classified into cluster k. In partition clustering algorithms, one of these values will be one and the rest will be zero. This represents the fact that these algorithms classify an individual into one and only one cluster. In fuzzy clustering, the membership is spread among all clusters. The probability of each object to be in each cluster can now be between zero and one, with the stipulation that the sum of their values is one. We call this a fuzzification of the cluster configuration. It has the advantage that it does not force every object into a specific cluster. It has the disadvantage that there is much more information to be interpreted.
Regression Clustering
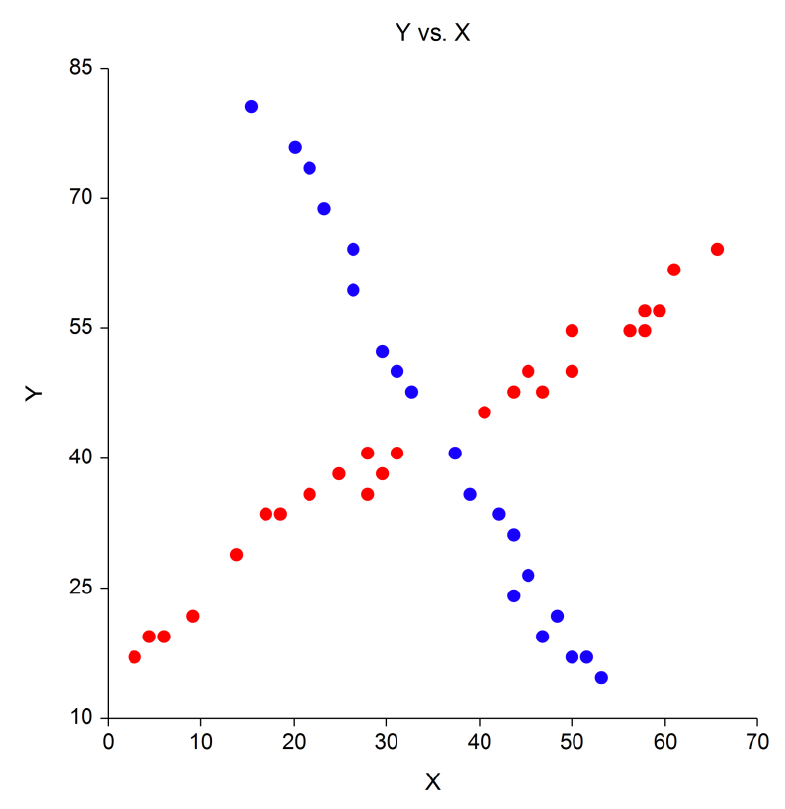
[Documentation PDF]The algorithm used in this procedure provides for clustering in the multiple regression setting in which you have a dependent variable Y and one or more independent variables, the X’s. The algorithm partitions the data into two or more clusters and performs an individual multiple regression on the data within each cluster. It is based on an exchange algorithm described in Spath.
Regression Exchange Algorithm
This algorithm is fairly simple to describe. The number of clusters, K, for a given run is fixed. The rows are randomly sorted into the groups to form K initial clusters. An exchange algorithm is applied to this initial configuration which searches for the rows of data that would produce a maximum decrease in a least-squares penalty function (that is, maximizing the increase in R-squared at each step). The algorithm continues until no beneficial exchange of rows can be found. The following chart shows data that were clustered using this algorithm. Notice how the two clusters actually intersect.Output from the NCSS Scatter Plot Procedure based on Regression Clustering Procedure Results