Mixed Models in NCSS

NCSS contains a general mixed models analysis procedure, as well as three specific case procedures. Use the links below to jump to a mixed models topic. To see how these tools can benefit you, we recommend you download and install the free trial of NCSS. Jump to:

Introduction
Technical Details
Mixed Models - General
Mixed Models – No Repeated Measures
Mixed Models – Repeated Measures
Mixed Models – Random Coefficients

Introduction

The Linear Mixed Model (or just Mixed Model) is a natural extension of the general linear model. Mixed models extend linear models by allowing for the addition of random effects, where the levels of the factor represent a random subset of a larger group of all possible levels (e.g., time of administration, clinic, etc.). For example, a two-factor linear model could be augmented to include a random block effect such as clinic or doctor since the clinic or doctor may be assumed to be a random realization from a distribution of clinics or doctors. Covariates (continuous) and/or nested effects can also be included in the mixed model to improve the accuracy of the fixed effect estimates. The Mixed Models procedures in NCSS can be used to analyze results from a wide variety of experimental designs in which the outcome (response) is continuous, including

Two-sample designs (replacing the t-test)
One-way layout designs (replacing one-way ANOVA)
Factorial designs (replacing factorial GLM)
Split-plot designs (replacing split-plot GLM)
Repeated-measures designs (replacing repeated-measures GLM)
Cross-over designs (replacing GLM)
Designs with covariates (replacing GLM)

The Mixed Models procedure can be used to test and estimate means (including pair-wise comparisons among levels), compare models, estimate variance-covariance matrix components, and produce graphs of means and repeated measurements of subjects. Examples are given in this chapter of models with only between-subjects factors, only within-subjects factors, and both between- and within-subjects factors. Analysis of covariance examples and multiple comparisons examples are also included. Mixed models have several advantages over traditional linear models. Just a few are listed here.

Specifying More Appropriate Variance-Covariance Structures for Longitudinal Data: The ability to fit complex covariance patterns provides more appropriate fixed effect estimates and standard errors.
Analysis Assuming Unequal Group Variances: Different variances can be fit for each treatment group.
Analysis of Longitudinal Data with Unequal Time Points: Mixed models allow for the analysis of data in which the measurements were made at random (varying) time points.
Analysis of Longitudinal Data with Missing Response Data: Problems caused by missing data in repeated measures and cross-over trials are eliminated.
Greater Flexibility in Modeling Covariates: Covariates can be modeled as fixed or random and more accurately represent their true contribution in the model.

Mixed models are particularly useful in medical studies where a wide variety of factors influence the response to a treatment of interest. For example, suppose that an experimental treatment is being administered to a group of patients desiring to lose weight. Traditional statistical methodologies (e.g., ANOVA, multiple regression, etc.) require that the treatments be given at the same time intervals for all patients in the group in order for the statistical analysis and conclusions to be accurate. What would happen if patients were not all able to receive the treatment at the same time intervals or if some patients missed some treatments? Traditional statistical approaches would no longer be valid since there are random events or components entering into the experiment. This is where mixed models techniques become useful. A mixed model would allow us to make inferences about the treatment by modeling and estimating the random components. Furthermore, mixed models allow us to make greater use of incomplete data, such as that obtained from patients who drop out or miss scheduled treatments. Traditional methods would exclude such individuals from the analysis, losing valuable information.

Technical Details

This page provides a general overview of the tools that are available in NCSS for analyzing mixed models. If you would like to examine the formulas and technical details relating to a specific NCSS procedure, click on the corresponding '[Documentation PDF]' link under each heading to load the complete procedure documentation. There you will find formulas, references, discussions, and examples or tutorials describing the procedure in detail.

Mixed Models - General

[Documentation PDF]

The Mixed Models – General procedure contains all the options available for mixed models in NCSS. It has the most flexibility and can be used to perform the analyses of each of the other 3 mixed models procedures. Because it is the most general, it is also the most complicated mixed model procedure. Specification of each option requires a fairly involved understanding of the procedure and mixed model concepts. It may be useful to determine which of the examples is most similar to your research situation, and then use the example to identify the needed procedure specification for your case. Here is a list of the examples associated with the Mixed Models – General procedure:

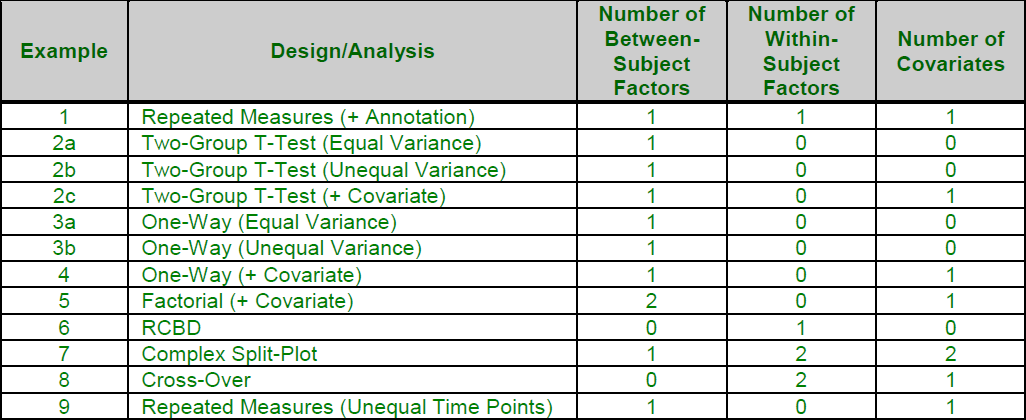These examples give a general idea of the breadth of analyses that are available using the Mixed Models procedure. Since the topic is so involved, we recommend that you view the documentation for this procedure, or download the free trial and go through the documentation and examples found there.

Mixed Models Example Dataset

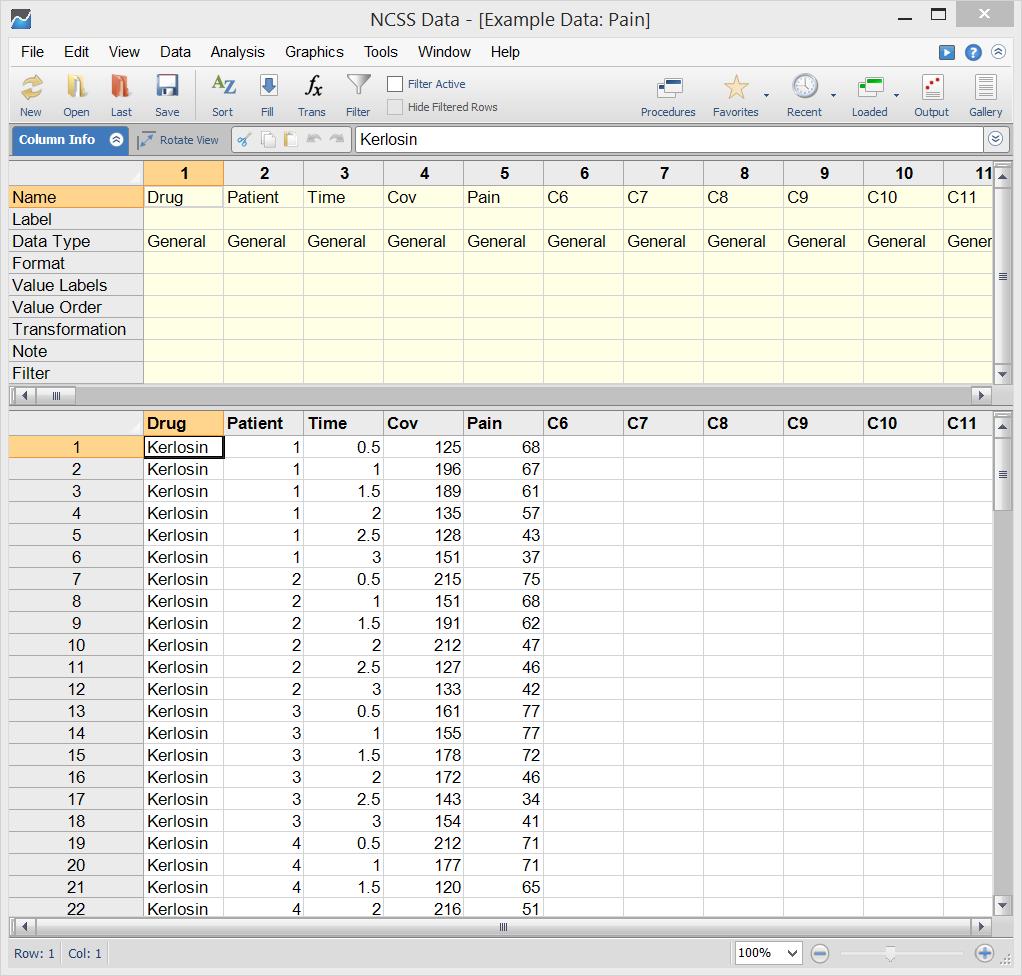
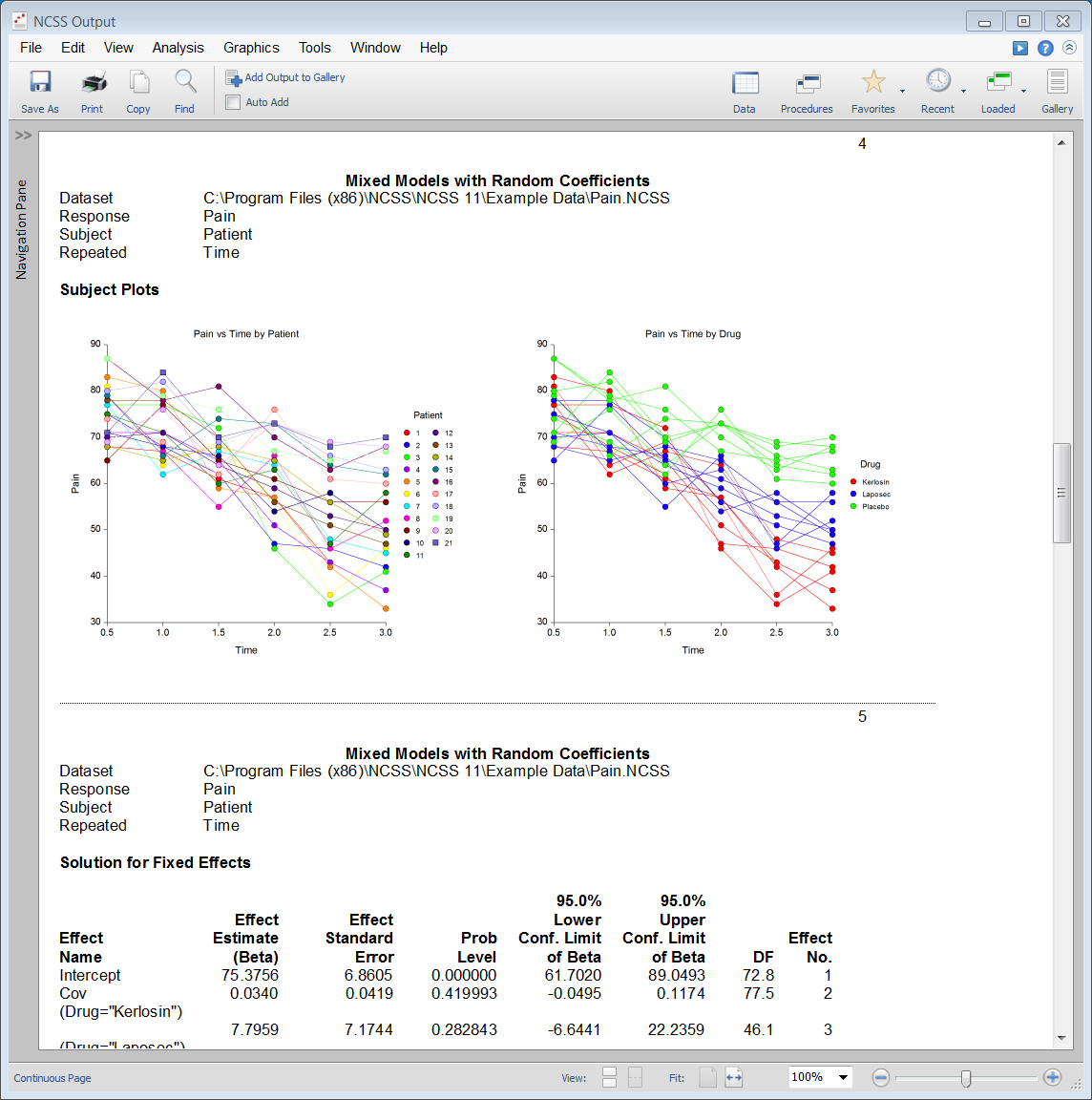
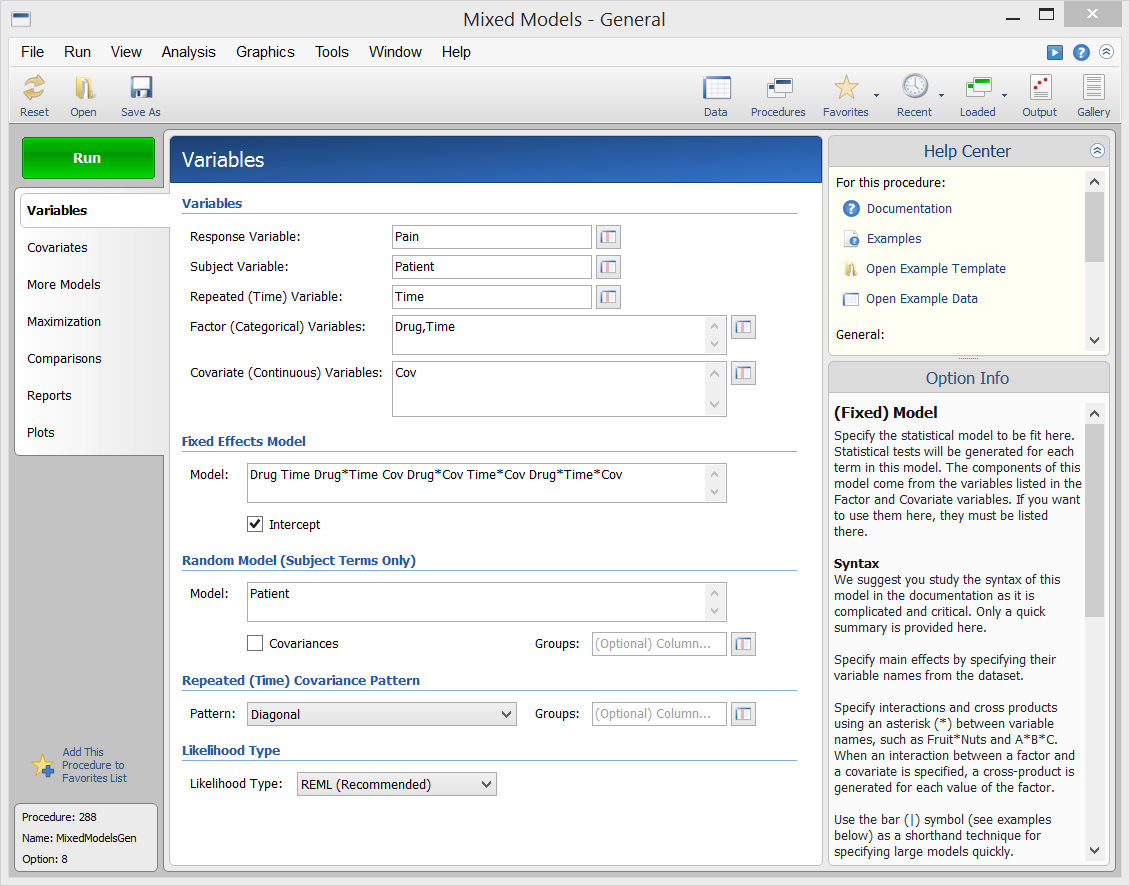
Example Setup (Variables Tab) of the Mixed Models - General Procedure

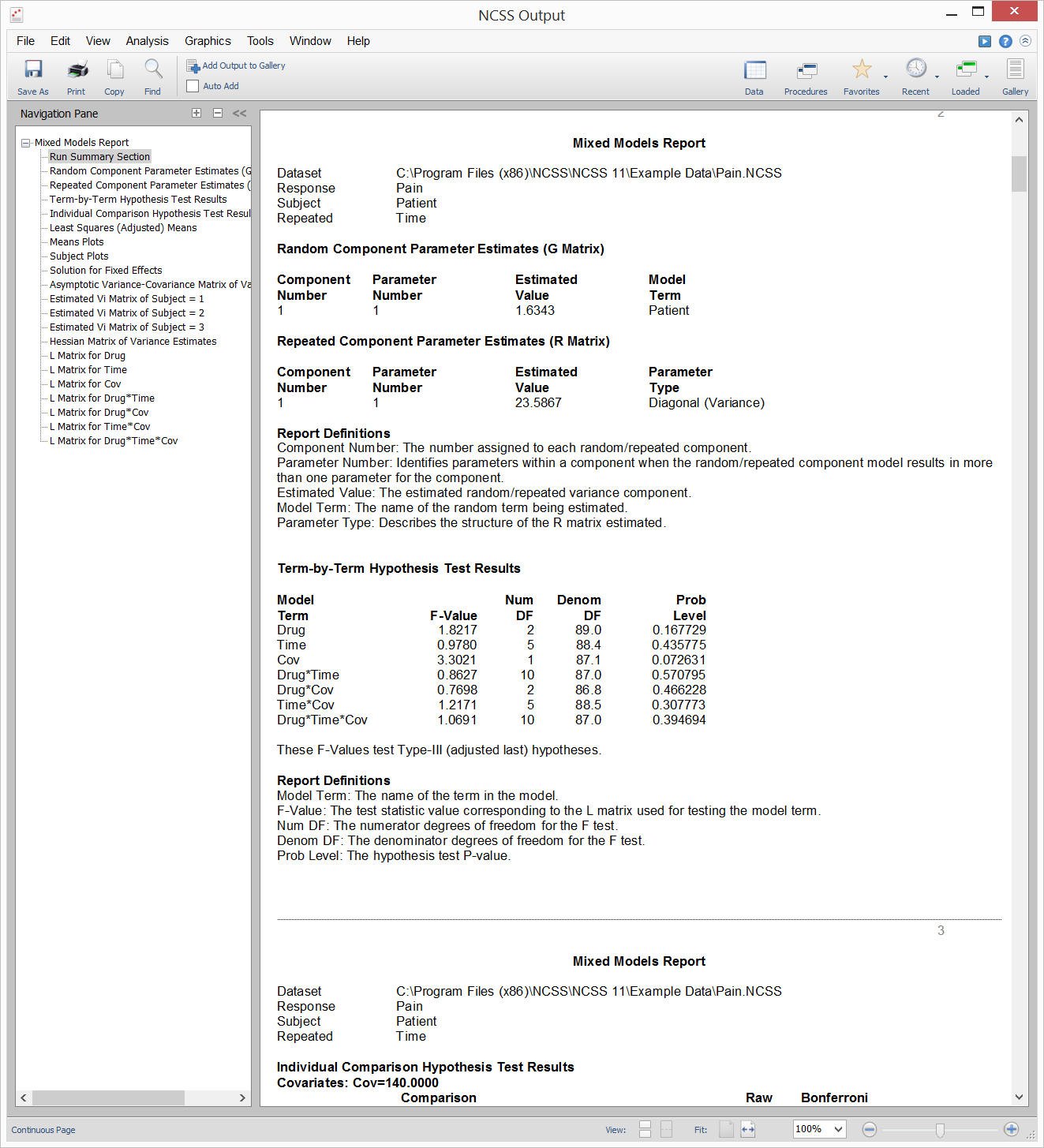
Example Output for the Mixed Models - General Procedure

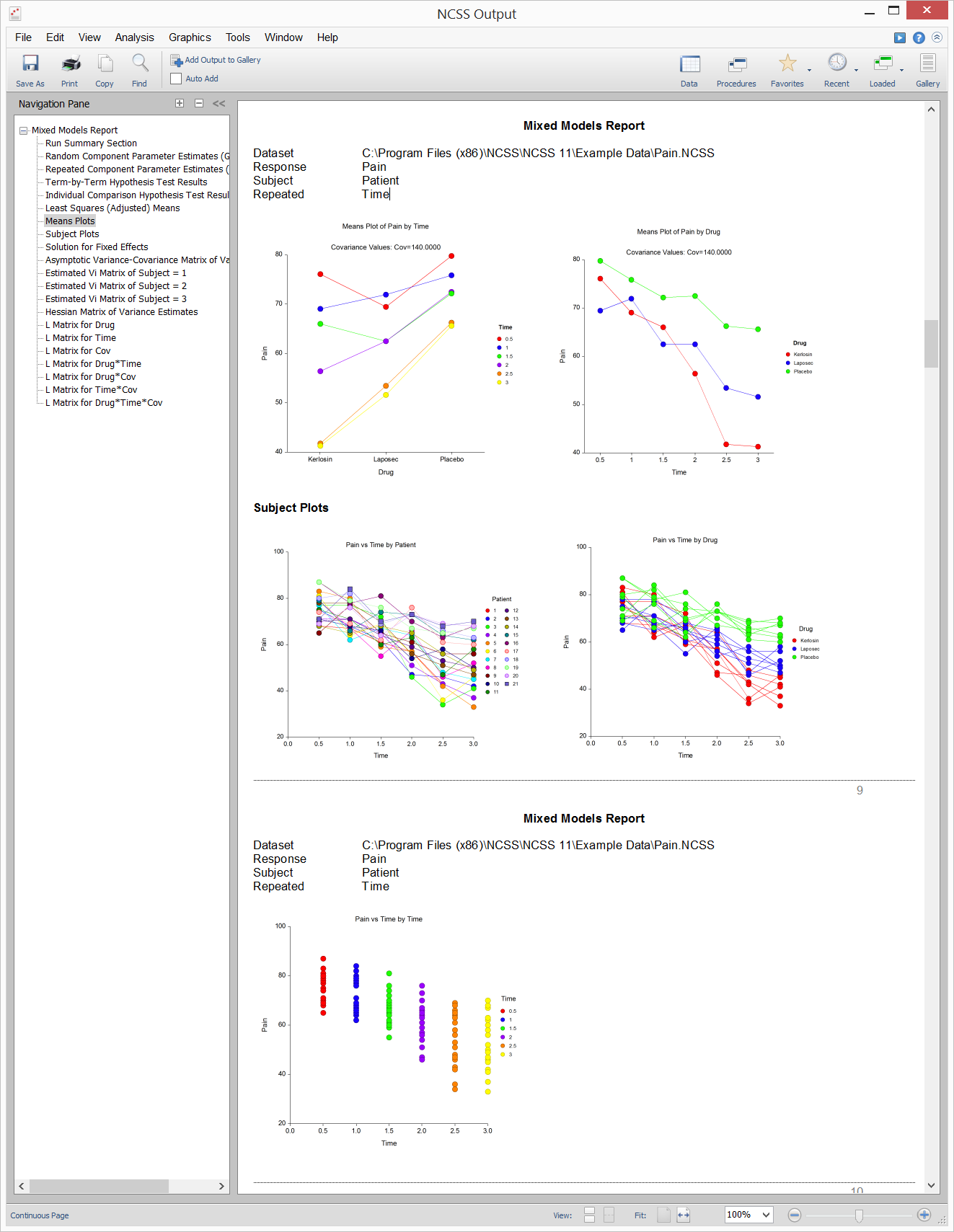
Example Plot Section Output for the Mixed Models - General Procedure

Mixed Models – No Repeated Measures

[Documentation PDF]

The Mixed Models – No Repeated Measures procedure is a simplification of the Mixed Models – General procedure to the case of fixed effects designs, such as factorial designs. This procedure is particularly useful when covariates are involved, or when you wish to model unequal variances across the levels of a factor. As the name of the procedure implies, this procedure is to be used when there is only one measurement per subject. While the same results could be obtained using the Mixed Models – General procedure, the Mixed Models – No Repeated Measures procedure has been developed to avoid the unneeded complexity of specification when there are not repeated measurements.

Mixed Models – Repeated Measures

[Documentation PDF]

The Mixed Models – Repeated Measures procedure is a simplification of the Mixed Models – General procedure to the case of repeated measures designs in which the outcome is continuous and measured at fixed time points. Typical designs that are analyzed with the Mixed Models – Repeated Measures procedure are

Split-plot designs
Repeated-measures designs
Cross-over designs
Repeated-measures designs with covariates

The Mixed Models – Repeated Measures procedure uses the same computation engine as the Mixed Models – General procedure, but is simplified to the case of repeated measures designs.

Mixed Models – Random Coefficients

[Documentation PDF]

The Mixed Models – Random Coefficients procedure is a simplification of the Mixed Models – General procedure to the case of random coefficients models. Random coefficients models are models in which the intercept and slope (regression coefficients) are generated for each subject. Because the subjects are randomly sampled from a population of subjects, the resulting models are called random coefficients models. Random coefficient models are generated in mixed models by including both the subject term and the subject*time interaction term as random effects in the model. Many more details about random coefficients models and using random coefficients models in NCSS are given in the Mixed Models – Random Coefficients chapter of the documentation.