Assurance in PASS
PASS contains over 50 assurance procedures, including assurance procedures for comparing means, proportions, survival, negative binomial rates, and Poisson rates. Each procedure is easy-to-use and validated for accuracy. A list of assurance procedures in PASS is given below. For more details about a procedure, we recommend you
download and install the free trial of the PASS software.
Jump to:
Assurance procedures in PASS:
- Assurance for Two-Sample T-Tests Assuming Equal Variance
- Assurance for Two-Sample Z-Tests Assuming Equal Variance
- Assurance for Two-Sample T-Tests Allowing Unequal Variance
- Assurance for Two-Sample T-Tests for Non-Inferiority Assuming Equal Variance
- Assurance for Two-Sample T-Tests for Superiority by a Margin Assuming Equal Variance
- Assurance for Two-Sample T-Tests for Equivalence Assuming Equal Variance
- Assurance for Two-Sample T-Tests for Non-Inferiority Allowing Unequal Variance
- Assurance for Two-Sample T-Tests for Superiority by a Margin Allowing Unequal Variance
- Assurance for Two-Sample T-Tests for Equivalence Allowing Unequal Variance
- -
- Assurance for Tests for Two Proportions
- Assurance for Non-Zero Null Tests for the Difference Between Two Proportions
- Assurance for Non-Inferiority Tests for the Difference Between Two Proportions
- Assurance for Superiority by a Margin Tests for the Difference Between Two Proportions
- Assurance for Equivalence Tests for the Difference Between Two Proportions
- Assurance for Non-Unity Null Tests for the Ratio of Two Proportions
- Assurance for Non-Unity Null Tests for the Odds Ratio of Two Proportions
- Assurance for Superiority by a Margin Tests for the Ratio of Two Proportions
- Assurance for Non-Inferiority Tests for the Ratio of Two Proportions
- Assurance for Superiority by a Margin Tests for the Odds Ratio of Two Proportions
- Assurance for Non-Inferiority Tests for the Odds Ratio of Two Proportions
- Assurance for Equivalence Tests for the Ratio of Two Proportions
- Assurance for Equivalence Tests for the Odds Ratio of Two Proportions
- -
- Assurance for Logrank Tests (Freedman)
- Assurance for Tests for Two Survival Curves Using Cox's Proportional Hazards Model
- Assurance for Non-Inferiority Tests for Two Survival Curves Using Cox's Proportional Hazards Model
- Assurance for Superiority by a Margin Tests for Two Survival Curves Using Cox's Proportional Hazards Model
- Assurance for Equivalence Tests for Two Survival Curves Using Cox's Proportional Hazards Model
- Assurance for Tests for the Difference of Two Hazard Rates Assuming an Exponential Model
- Assurance for Non-Inferiority Tests for the Difference of Two Hazard Rates Assuming an Exponential Model
- Assurance for Superiority by a Margin Tests for the Difference of Two Hazard Rates Assuming an Exponential Model
- Assurance for Equivalence Tests for the Difference of Two Hazard Rates Assuming an Exponential Model
- -
- Assurance for Tests for the Ratio of Two Negative Binomial Rates
- Assurance for Non-Inferiority Tests for the Ratio of Two Negative Binomial Rates
- Assurance for Superiority by a Margin Tests for the Ratio of Two Negative Binomial Rates
- Assurance for Equivalence Tests for the Ratio of Two Negative Binomial Rates
- -
- Assurance for Tests for Two Means in a Cluster-Randomized Design
- Assurance for Non-Inferiority Tests for Two Means in a Cluster-Randomized Design
- Assurance for Superiority by a Margin Tests for Two Means in a Cluster-Randomized Design
- Assurance for Equivalence Tests for Two Means in a Cluster-Randomized Design
- Assurance for Tests for Two Proportions in a Cluster-Randomized Design
- Assurance for Non-Zero Null Tests for the Difference of Two Proportions in a Cluster-Randomized Design
- Assurance for Non-Inferiority Tests for the Difference of Two Proportions in a Cluster-Randomized Design
- Assurance for Superiority by a Margin Tests for the Difference of Two Proportions in a Cluster-Randomized Design
- Assurance for Equivalence Tests for the Difference of Two Proportions in a Cluster-Randomized Design
- Assurance for Logrank Tests in a Cluster-Randomized Design
- -
- Assurance for Tests for the Difference Between Two Poisson Rates
- Assurance for Tests for the Ratio of Two Poisson Rates
- Assurance for Non-Inferiority Tests for the Ratio of Two Poisson Rates
- Assurance for Superiority by a Margin Tests for the Ratio of Two Poisson Rates
- Assurance for Equivalence Tests for the Ratio of Two Poisson Rates
- -
- Assurance for Non-Inferiority Tests for Vaccine Efficacy using the Ratio of Two Proportions
- Assurance for Superiority by a Margin Tests for Vaccine Efficacy using the Ratio of Two Proportions
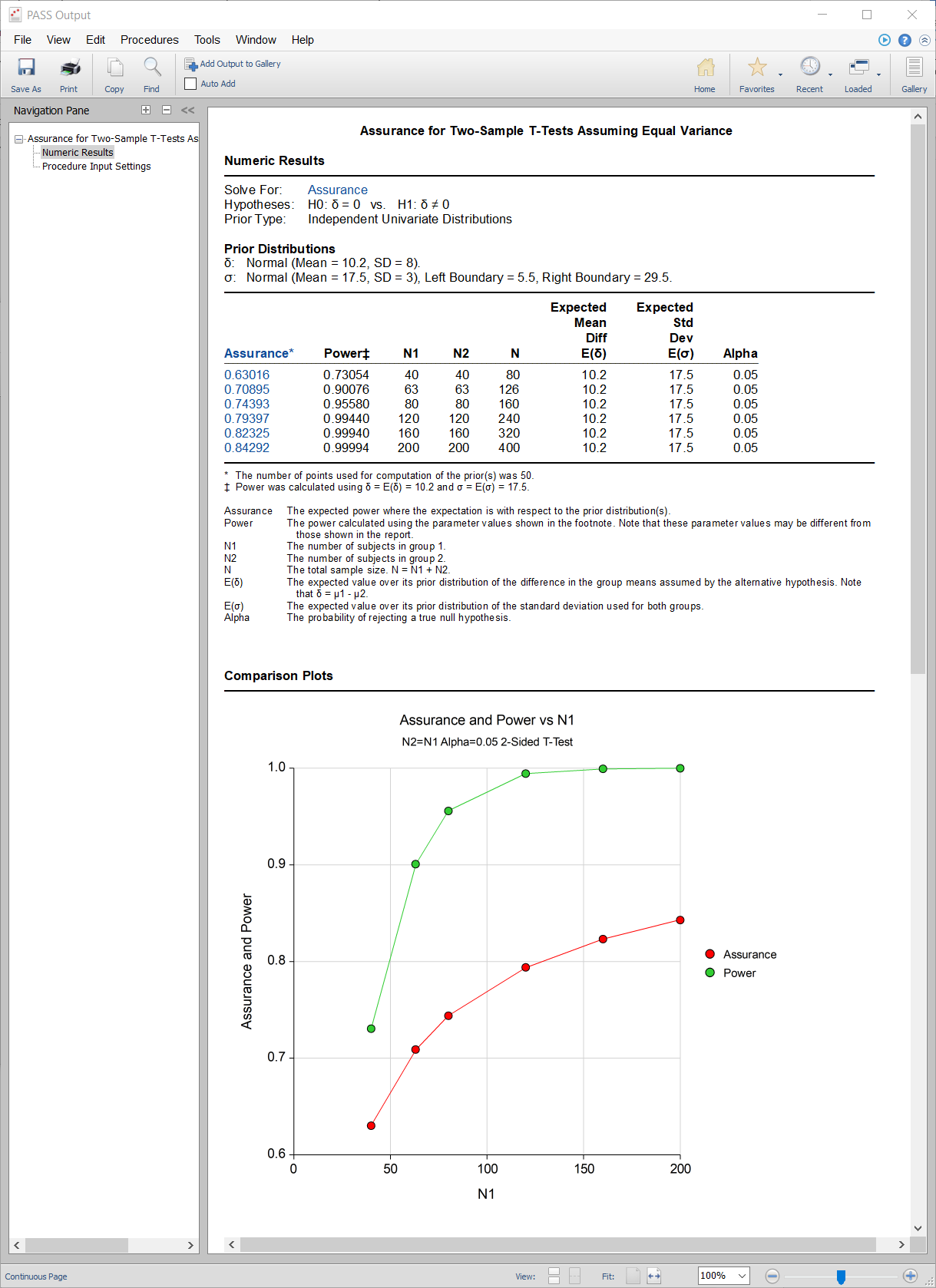
Assurance
The assurance of a design is the expected value of the power with respect to one or more prior distributions of the design parameters. Assurance is also referred to as Bayesian assurance, expected power, average power, statistical assurance, hybrid classical-Bayesian procedure, or probability of success.
The power of a design is the probability of rejecting the null hypothesis, conditional on a given set of design attributes, such as the test statistic, the significance level, the sample size, and the effect size to be detected. As the effect size parameters are typically unknown quantities, the stated power may be very different from the true power if the specified parameter values are inaccurate.
While power is conditional on individual design parameter values, and is highly sensitive to those values, assurance is the average power across a presumed prior distribution of the effect size parameters. Thus, assurance adds a Bayesian element to the frequentist framework, resulting in a hybrid approach to the probability of trial or study success. It should be noted that when it comes time to perform the statistical test on the resulting data, these methods for calculating assurance assume that the traditional (frequentist) tests will be used.
The next section describes some of the ways in which the prior distributions for effect size parameters may be determined.
Elicitation
In order to calculate assurance, a suitable prior distribution for the effect size parameters must be determined. This process is called the elicitation of the prior distribution.
The elicitation may be as simple as choosing a distribution that seems plausible for the parameter(s) of interest, or as complex as combining the informed advice of several experts based on experience in the field, available pilot data, or previous studies. The accuracy of the assurance value depends on the accuracy of the elicited prior distribution. The assumption (or hope) is that an informed prior distribution will produce a more accurate estimate of the probability of trial success than a single value estimate. Because clinical trials and other studies are often costly, many institutions now routinely require an elicitation step.
Two reference texts that focus on elicitation are O’Hagan, Buck, Daneshkhah, Eiser, Garthwaite, Jenkinson, Oakley, and Rakow (2006) and Dias, Morton, and Quigley (2018).
List of Available Univariate Prior Distributions
Below is a list of the univariate prior distributions that may be used for any of the applicable parameters when specifying a prior distribution in an assurance procedure in PASS:
- No Prior
- Beta (Shape 1, Shape 2, a, c)
- Gamma (Shape, Scale)
- Inverse-Gamma (Shape, Scale)
- Logistic (Location, Scale)
- Lognormal (Mean, SD)
- LogT (Mean, SD)
- Normal (Mean, SD)
- T (Mean, SD, DF)
- Triangle (Mode, Min, Max)
- Uniform (Min, Max)
- Weibull (Shape, Scale)
- Custom (Values and Probabilities in Spreadsheet)
An Example Setup and Output
When the PASS software is first opened, the user is presented with the PASS Home window. From this window the desired procedure is selected from the menus, the category tree on the left, or with a procedure search. The procedure opens and the desired entries are made. When you click the Calculate button the results are produced. You can easily navigate to any part of the output with the navigation pane on the left.
PASS Home Window
Procedure Window for Assurance
PASS Output Window