Sample Size for Correlation in PASS

PASS contains several procedures for sample size calculation and power analysis for correlation, including tests for one and two correlations, confidence intervals for one correlation, and tests for intraclass correlation. PASS also has procedures that compute sample size and power for testing one and two coefficient alphas, testing kappa for the agreement between two raters, and Lin’s concordance correlation coefficient. Each procedure is easy-to-use and validated for accuracy. Use the links below to jump to a correlation topic. Only a brief summary is given for each procedure. For more details about a topic, we recommend you download and install the free trial of the PASS software and utilize its correlation software.

Jump to:

• Introduction
• Technical Details
• An Example Setup and Output
• Tests for One Correlation
• Tests for Two Correlations
• Confidence Intervals for One Correlation
• Tests for Intraclass Correlation
• Tests for One Coefficient (Cronbach’s) Alpha
• Tests for Two Coefficient (Cronbach’s) Alphas
• Kappa Test for Agreement Between Two Raters
• Lin’s Concordance Correlation Coefficient
• Point Biserial Correlation Tests
• Spearman’s Rank Correlation Tests with Simulation

Introduction

For most of the correlation procedures in PASS software, the user may choose to solve for sample size, power, or the correlation value. In the case of confidence intervals, one could solve for sample size or the distance to the confidence limit. In a typical correlation procedure where the goal is to estimate the sample size, the user enters power, alpha, and values related to correlation. The procedure is run and the output shows a summary of the entries as well as the sample size estimate(s). A summary statement is given, as well as references to the articles from which the formulas for the result were obtained. For many of the parameters (e.g., power, alpha, sample size, correlation, etc.), multiple values may be entered in a single run. When this is done, estimates are made for every combination of entered values. A numeric summary of these results is produced along with easy-to-read sample size or power curve graphs.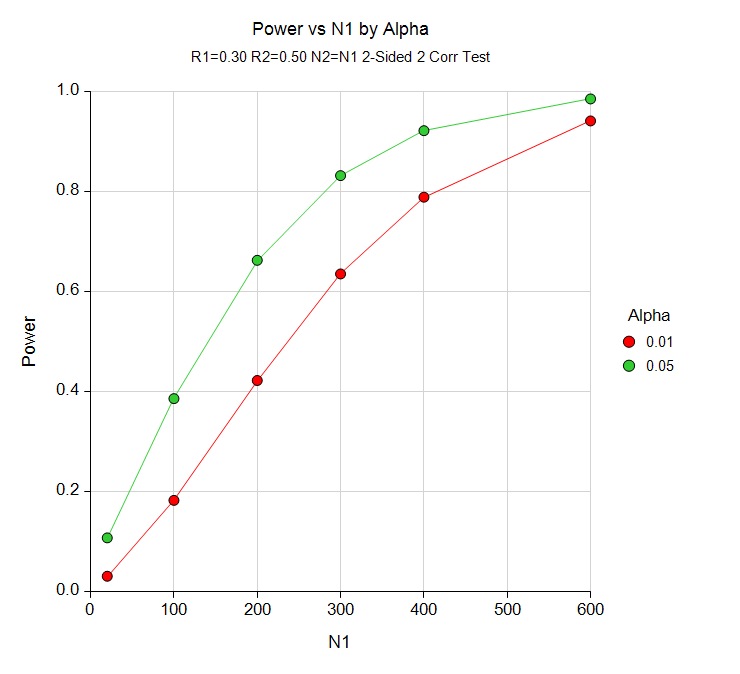

Technical Details

This page provides a brief description of the tools that are available in PASS software for sample size correlation and power analysis. If you would like to examine the formulas and technical details relating to a specific PASS procedure, we recommend you download and install the free trial of the software, open the desired correlation procedure, and click on the help button in the top right corner to view the complete documentation of the procedure. There you will find summaries, formulas, references, discussions, technical details, examples, and validation against published articles for the procedure.

An Example Setup and Output

When the PASS software is first opened, the user is presented with the PASS Home window. From this window the desired procedure is selected from the menus, the category tree on the left, or with a procedure search. The procedure opens and the desired entries are made. When you click the Calculate button the results are produced. You can easily navigate to any part of the output with the navigation pane on the left.

PASS Home Window

Procedure Window for Testing Two Correlations

PASS Output Window

Sample Size for Tests for One Correlation

The correlation coefficient, ρ (rho), is a popular statistic for describing the strength of the relationship between two variables. The correlation coefficient is the slope of the regression line between two variables when both variables have been standardized by subtracting their means and dividing by their standard deviations. The correlation ranges between negative one and one.

When ρ is used as a descriptive statistic, no special distributional assumptions need to be made about the variables (Y and X) from which it is calculated. When hypothesis tests are made, you assume that the observations are independent and that the variables are distributed according to the bivariate-normal density function. However, as with the t-test, tests based on the correlation coefficient are robust to moderate departures from this normality assumption.

The population correlation ρ is estimated by the sample correlation coefficient r. Note we use the symbol R on the screens and printouts to represent the population correlation.

The Tests for One Correlation procedure in PASS provides sample size and power calculations for testing the null hypothesis that an alternative correlation, ρ₁, is equal to the baseline correlation, ρ₀. Usually ρ₀ = 0.

Sample Size for Tests for Two Correlations

The correlation coefficient (or correlation), ρ, is used to describe the strength of association between two variables. The correlation coefficient is the slope of the regression line between two variables when both variables have been standardized. It ranges between negative one and one. The Tests for Two Correlations procedure in PASS computes power and sample size for the case where you want to test the difference between two correlations, each coming from a separate sample. The null hypothesis is H₀: ρ₁ = ρ₂.

Since the correlation is the standardized slope between two variables, you could also apply this procedure to the case where you want to test whether the slopes in two groups are equal.

Sample Size for Confidence Intervals for One Correlation

The Confidence Intervals for One Correlation procedure in PASS calculates the sample size necessary to achieve a specified interval width or distance from the sample correlation to the interval limit at a stated confidence level for a confidence interval for one correlation. This procedure assumes that the correlation of the future sample will be the same as the correlation that is specified. If the sample correlation is different from the one specified when running this procedure, the interval width may be narrower or wider than specified.

Sample Size for Tests for Intraclass Correlation

The intraclass correlation coefficient is often used as an index of reliability in a measurement study. In these studies, there are N observations made on each of K individuals. These individuals represent a factor observed at random. This design arises when K subjects are each rated by N raters.

The intraclass correlation coefficient may be thought of as the correlation between any two observations made on the same subject. When this correlation is high, the observations on a subject tend to match, and the measurement reliability is “high.”

The Tests for Intraclass Correlation procedure in PASS calculated the power and sample size for testing the null hypothesis H₀: ρ = ρ₀ versus the alternative H₁: ρ > ρ₀, where the intraclass correlation, ρ, is defined as

ρ = σ_a² / σ_a² + σ_e²

where σ_a² is the variance of the random subject effects and σ_e² is the variance of the measurement errors.

Sample Size for Tests for One Coefficient (Cronbach’s) Alpha

Coefficient alpha, or Cronbach’s alpha, ρ, is a measure of the reliability of a scale consisting of k parts. The k parts usually often represent k items on a questionnaire or k raters. The Tests for One Coefficient Alpha procedure in PASS calculates power and sample size for testing the null hypothesis H₀: ρ = ρ₀ versus the alternative H₁: ρ > ρ₀ or H₁: ρ ≠ ρ₀. In practice, the null value, ρ₀, is often set as zero.

Sample Size for Tests for Two Coefficient (Cronbach’s) Alphas

The Tests for Two Coefficient Alphas procedure in PASS calculates power and sample size for testing whether two coefficient alphas are different when the two samples are either dependent or independent using the null hypothesis H₀: ρ₁ = ρ₂ versus the alternative H₁: ρ₁ > ρ₂ or H₁: ρ₁ ≠ ρ₂.

Sample Size for Kappa Test for Agreement Between Two Raters

The Kappa Test for Agreement Between Two Raters procedure in PASS computes power and sample size for the test of agreement between two raters using the kappa statistic. The null hypothesis is H₀: κ = κ₁ and the alternative is H₁: κ > κ₁ or H₁: κ ≠ κ₁.

Power calculations are based on ratings for k categories from two raters or judges. The user is able to vary category frequencies on a single run of the procedure to analyze a wide range of scenarios all at once.

Sample Size for Lin’s Concordance Correlation Coefficient

Lin’s concordance correlation coefficient (CCC) is the concordance between a new test or measurement (Y) and a gold standard test or measurement (X). This statistic quantifies the agreement between these two measures of the same variable (e.g. chemical concentration).

Like a correlation, CCC ranges from -1 to 1, with perfect agreement at 1. It cannot exceed the absolute value of ρ, Pearson’s correlation coefficient between Y and X. It can be legitimately calculated on as few as ten observations.

The Lin’s Concordance Correlation Coefficient procedure in PASS calculates power and sample size for testing the null hypothesis H₀: CCC ≤ CCC₀ against the alternative H₁: CCC > CCC₀.

Sample Size for Point Biserial Correlation Tests

The point biserial correlation coefficient is the product-moment correlation calculated between a continuous random variable (Y) and a binary random variable (X). This correlation is related to, but different from, the biserial correlation proposed by Karl Pearson. In psychology, the point biserial correlation is often used as a measure of the degree of association between a trait or attribute and a measureable characteristic such as an ability to accomplish something.

When ρ is used as a descriptive statistic, no special distributional assumptions need to be made about the variables (Y and X). When hypothesis tests are made, it is assumed that the observation pairs are independent and that the values of Y are distributed normally conditional on the value of X. The distribution of Y when X =1 is normal with mean μ1 and variance σ2, while the distribution of Y when X = 0 is normal with mean μ0 and variance also σ2.

If X is the result of a Bernoulli trial with probability of success (X = 1) p, then the design is said to be random. If X is set in advance, then the design is said to be fixed.

The Point Biserial Correlation Tests procedure in PASS calculates power and sample size for testing a point biserial correlation coefficient against a given null-hypothesized value.

Sample Size for Spearman’s Rank Correlation Tests with Simulation

This procedure analyzes the power and significance level of Spearman’s Rank Correlation significance test using
Monte Carlo simulation. This test is used to test whether the rank correlation is non-zero. For each scenario that is
set up, two simulations are run. One simulation estimates the significance level and the other estimates the power.

Spearman’s rho, ρ_s, is a popular statistic for describing the strength of the monotonic relationship between two
variables. It ranges between plus and minus one.