Sample Size for Survival Analysis Tests in PASS

PASS contains over 25 tools for sample size estimation and power analysis of survival methods, including logrank tests, non-inferiority, group-sequential, and conditional power, among others. Each procedure is easy-to-use and is carefully validated for accuracy. If you need help on how to use PASS sample size estimation software, use the links below to jump to a survival topic. For each procedure, only a brief summary of the procedure is given. For more details about a particular procedure, we recommend you download and install the free trial to really understand how to use PASS software. Jump to:

• Introduction
• Technical Details
• An Example Setup and Output
• Logrank Tests for Survival Curve Inequality
• Other Tests for Survival Curve Inequality
• Non-Inferiority Tests for Two Survival Curves
• Equivalence Tests for Two Survival Curves
• Superiority by a Margin Tests for Two Survival Curves
• Group-Sequential Logrank Tests
• Conditional Power of Logrank Tests
• Cox Regression
• One-Sample Tests for Exponential Hazard Rate

Introduction

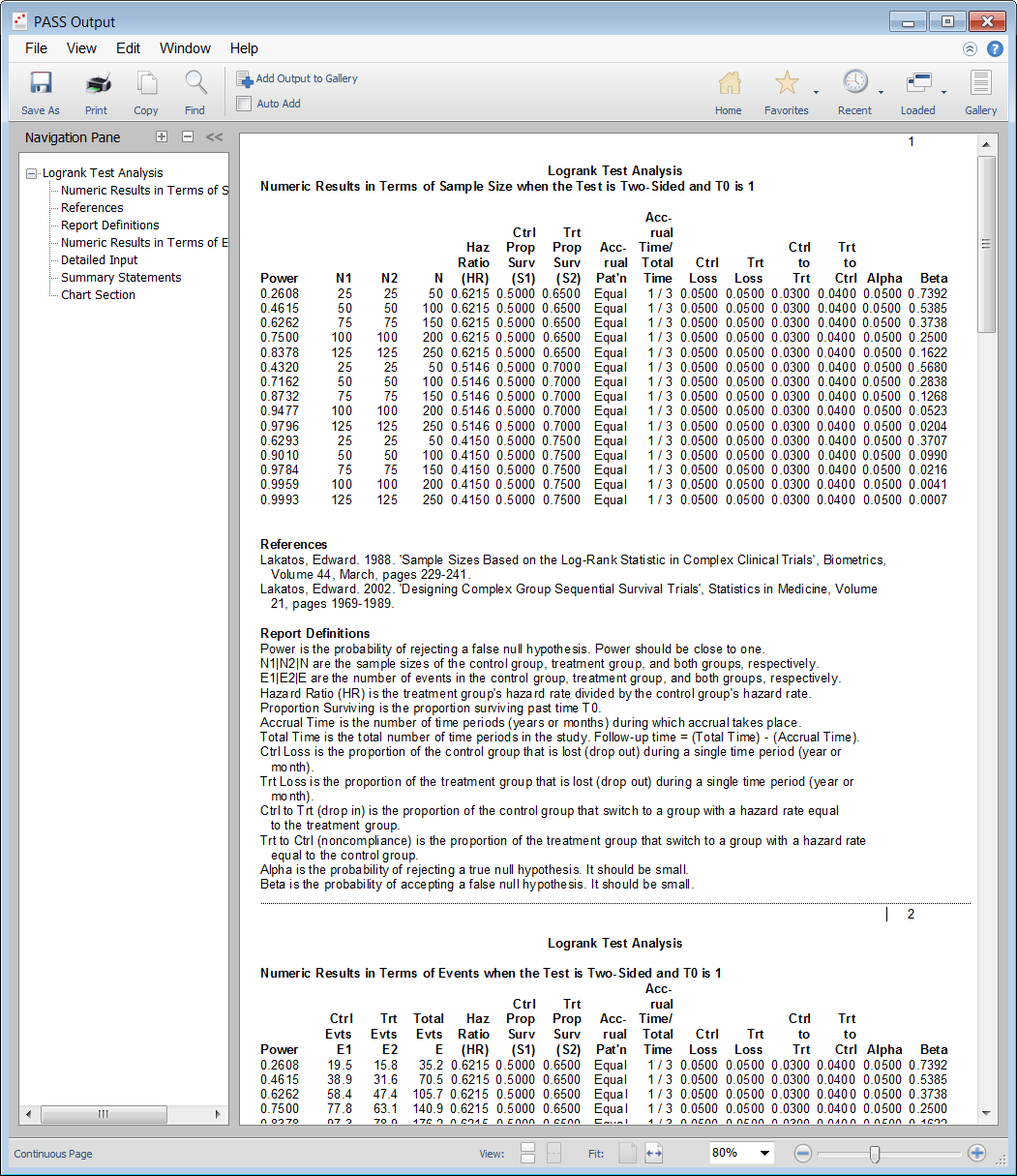
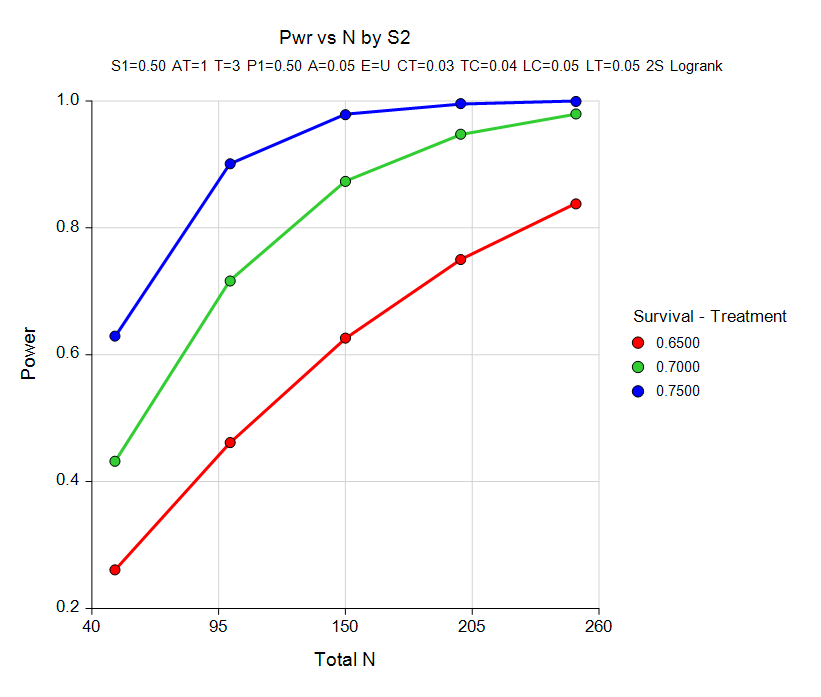
For most of the sample size procedures in PASS for survival, the user may choose to solve for sample size, power, or the population effect size in some manner. In a typical survival test procedure where the goal is to estimate the sample size, the user enters power, alpha, and the desired population survival parameters. The procedure is run and the output shows a summary of the entries as well as the sample size estimate. A summary statement is given, as well as references to the articles from which the formulas for the result were obtained. For many of the parameters (e.g., power, alpha, sample size, survival, etc.), multiple values may be entered in a single run. When this is done, estimates are made for every combination of entered values. A numeric summary of these is results is produced as well as easy-to-read sample size or power curve graphs.

Technical Details

This page provides a brief description of the tools that are available in PASS for power and sample size analysis of survival methods. If you would like to examine the formulas and technical details relating to a specific PASS procedure, we recommend you download and install the free trial of the software, open the desired survival procedure, and click on the help button in the top right corner to view the complete documentation of the procedure. There you will find summaries, formulas, references, discussions, technical details, examples, and validation against published articles for the procedure.

An Example Setup and Output

When the PASS software is first opened, the user is presented with the PASS Home window. From this window the desired procedure is selected from the menus, the category tree on the left, or with a procedure search. The procedure opens and the desired entries are made. When you click the Calculate button the results are produced. You can easily navigate to any part of the output with the navigation pane on the left.

PASS Home Window

Logrank Tests Procedure Window

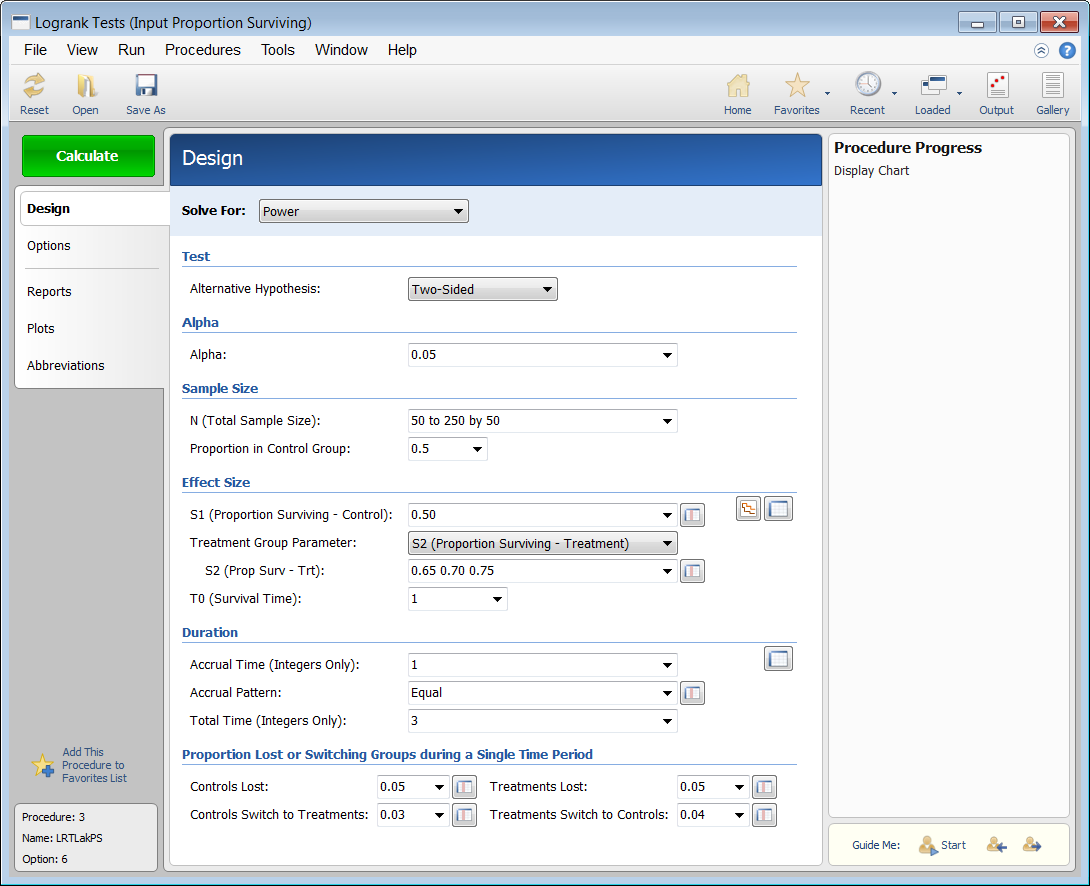
PASS Output Window

Power Curve for the Logrank Tests Procedure

Sample Size for Logrank Tests for Survival Curve Inequality

There are several procedures in PASS for determining sample size or power for inequality tests of two survival curves:

• Logrank Tests (Input Hazard Rates)
• Logrank Tests (Input Median Survival Times)
• Logrank Tests (Input Proportion Surviving)
• Logrank Tests (Input Mortality)
• Tests for Two Survival Curves Using Cox’s Proportional Hazards Model
• Tests for the Difference of Two Hazard Rates Assuming an Exponential Model
• Logrank Tests Accounting for Competing Risks

For several of these procedures, you may specify the proportion of individuals in the control and treatment groups, the accrual time, and the total time. In the first four, you can also specify an accrual pattern, and proportions of subjects lost to follow-up or switching groups. Where appropriate, the number of events is also reported.

Sample Size for Other Tests for Survival Curve Inequality using Simulation

A simulation based procedure is used to evaluate sample size and power for each of the following tests for comparing two survival curves:

• Logrank
• Gehan-Wilcoxon
• Taron-Ware
• Peto-Peto
• Modified Peto-Peto
• Fleming-Harrington

Sample Size for Non-Inferiority Tests for Two Survival Curves

The sample size and power analysis procedures in PASS for non-inferiority of two survival curves are:

• Non-Inferiority Logrank Tests
• Non-Inferiority Tests for Two Survival Curves Using Cox’s Proportional Hazards Model
• Non-Inferiority Tests for the Difference of Two Hazard Rates Assuming an Exponential Model

The first of the three procedures computes the sample size and power for non-inferiority tests under the assumption of proportional hazards. Accrual time and follow-up time are included among the parameters to be set. The non-inferiority logrank test is the test that is anticipated for data analysis. The Cox’s Proportional Hazards Model procedure is documented in Chow, Shao, and Wang (2008) which summarizes the work of Schoenfeld (1981, 1983). The exponential model procedure is based on the unconditional method of Chow, Shao, and Wang (2008) which, in turn, is based on the conditional methods of Lachin and Foulkes (1986). The conditional procedure does not extend to non-inferiority, non-zero null, or equivalence tests as easily as the unconditional method does.

Sample Size for Equivalence Tests for Two Survival Curves

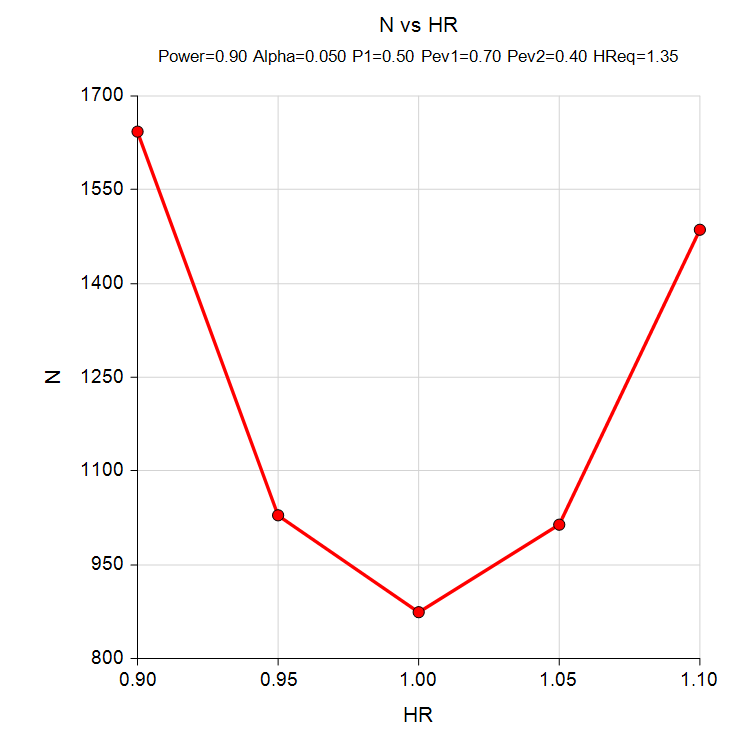
There are two survival equivalence procedures in PASS. The first procedure uses the Cox's proportional hazards model and the second assumes an exponential model.

Sample Size Curve for Survival Equivalence with Hazard Ratio on X Axis

Sample Size for Superiority by a Margin Tests for Two Survival Curves

There are two survival procedures for showing superiority by a margin in PASS. The first procedure uses the Cox's proportional hazards model and the second assumes an exponential model.

Sample Size for Group-Sequential Logrank Tests

In PASS, there is an analytic procedure for group-sequential logrank tests as well as four simulation procedures. The simulation procedures differ only in the survival input (hazard rates, median survival times, proportion surviving, or mortality). The following test methods are available in the simulation procedures:

• Logrank
• Gehan-Wilcoxon
• Taron-Ware
• Peto-Peto
• Modified Peto-Peto
• Fleming-Harrington

A variety of spending function options are available in the simulation procedures, including Hwang-Shi-DeCani, O’Brien-Fleming, and Pocock types. Either the T-test or the Mann-Whitney-Wilcoxon test may be examined. For one-sided tests, significance and futility boundaries can be produced. The spacing of the looks can be equal or custom specified. The distributions of each of the groups under the null and alternative hypotheses can be specified directly using over ten distributions including normal, exponential, Gamma, Uniform, Beta, and Cauchy. Boundaries can also be input directly to verify alpha- and/or beta-spending properties. Futility boundaries can be binding or non-binding.

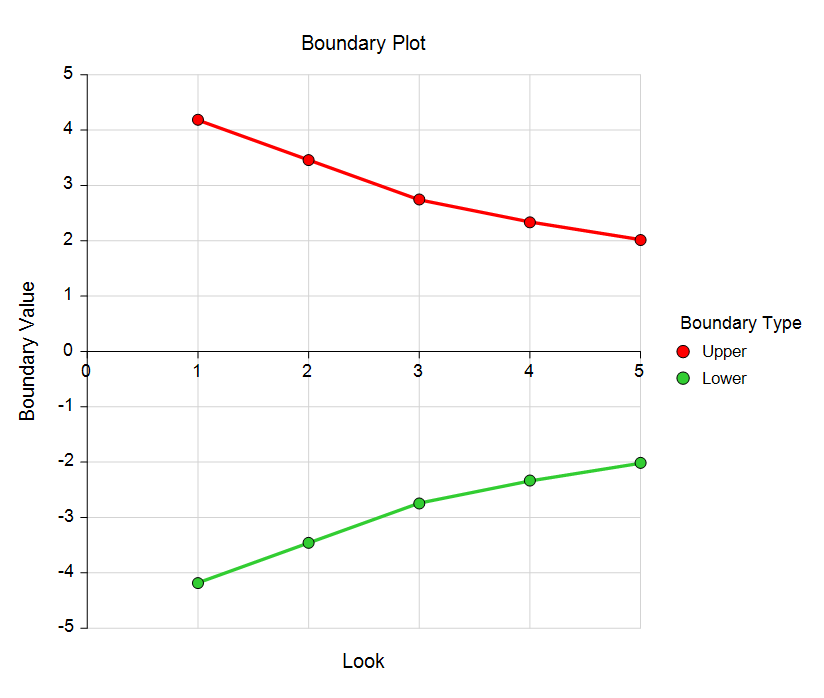
Group-Sequential Logrank Test Boundary Plot with 5 Looks

Sample Size for Group-Sequential Tests for Two Hazard Rates (Simulation)

This procedure can be used to determine power, sample size and/or boundaries for group-sequential Z-tests comparing the survival curves of two groups. This methodology assumes an underlying Exponential model. For one- and two-sided tests, efficacy and/or futility boundaries can be generated. The spacing of the stages can be equal or custom specified. Individual stages may also be skipped. Boundaries can be computed based on popular alpha- and beta-spending functions (O’Brien-Fleming Analog, Pocock Analog, Hwang-Shih-DeCani Gamma family, linear) or custom spending functions, or boundaries may be input directly, if desired. Futility boundaries can be binding or non-binding. Corresponding P-Value boundaries are given for each boundary statistic. Alpha and/or beta spent at each stage is reported. Plots of boundaries are also produced. This procedure is used as the planning tool for determining sample size and initial boundaries. Stage data, as it is obtained, can be evaluated using the companion procedure Group-Sequential Analysis for Two Hazard Rates. The companion procedure also gives the option for sample-size re-estimation and updated boundaries for current-stage information. In that procedure, simulation can be used to evaluate boundary-crossing probabilities given the current stage results.

Sample Size for Group-Sequential Non-Inferiority Tests for Two Hazard Rates (Simulation)

This procedure can be used to determine power, sample size and/or boundaries for group-sequential Z-tests comparing the survival curves of two groups, with a non-inferiority margin. Stage data, as it is obtained, can be evaluated using the companion procedure Group-Sequential Non-Inferiority Analysis for Two Hazard Rates. The companion procedure also gives the option for sample-size re-estimation and updated boundaries for current-stage information.

Sample Size for Group-Sequential Superiority by a Margin Tests for Two Hazard Rates (Simulation)

This procedure can be used to determine power, sample size and/or boundaries for group-sequential Z-tests comparing the survival curves of two groups, with a superiority margin. Stage data, as it is obtained, can be evaluated using the companion procedure Group-Sequential Superiority by a Margin Analysis for Two Hazard Rates. The companion procedure also gives the option for sample-size re-estimation and updated boundaries for current-stage information.

Sample Size for Conditional Power of Logrank Tests

In sequential designs, one or more intermediate analyses of the emerging data are conducted to evaluate whether the experiment should be continued. This may be done to conserve resources or to allow a data monitoring board to evaluate safety and efficacy when subjects are entered in a staggered fashion over a long period of time. Conditional power (a frequentist concept) is the probability that the final result will be significant, given the data obtained up to the time of the interim look. Predictive power (a Bayesian concept) is the result of averaging the conditional power over the posterior distribution of effect size. Both of these methods fall under the heading of stochastic curtailment techniques. This procedure computes conditional and predicted power for the case when a logrank test is used to compare the hazard rate of a treatment group to that of a control group. Conditional power procedures are also available in PASS for the case of Non-Inferiority and Superiority by a Margin.

Sample Size for Cox Regression

Cox proportional hazards regression models the relationship between the hazard function λ(t|X) of survival time and k covariates using the formula

log(λ(t|X) / λ₀(t|X)) = β₁X₁ + β₂X₂ + ... + β_kX_k

where λ₀(t|X) is the baseline hazard. Note that the covariates may be discrete or continuous. The Cox Regression procedure in PASS calculates power and sample size for testing the hypothesis that β₁=0 versus the alternative that β₁=B . Note that β₁ is the change in log hazard for a one-unit change in X₁ when the rest of the covariates are held constant. The procedure assumes that this hypothesis will be tested using the Wald (or score) statistic.

Sample Size for One-Sample Tests for Exponential Hazard Rate

This module computes the sample size and power of the one-sample exponential hazard rate test which is used to compare the hazard rate of a single treatment group to that of a historic control. This test is often adopted in clinical phase-II trials with survival endpoints. Accrual time, follow-up time, and hazard rates are parameters that can be set.