Sample Size for Variances and Standard Deviations in PASS
PASS contains a number of procedures for sample size calculation and power analysis for standard deviations and variances, including tests for one and two variances, confidence intervals for one variance, confidence intervals for the ratio two variances, and confidence intervals for one standard deviation. Each procedure is easy-to-use and validated for accuracy. Use the links below to jump to a correlation topic. Only a brief summary is given for each standard deviation sample size procedure. For more details about a topic, we recommend you
download and install the free trial of the software.
Jump to:
Introduction
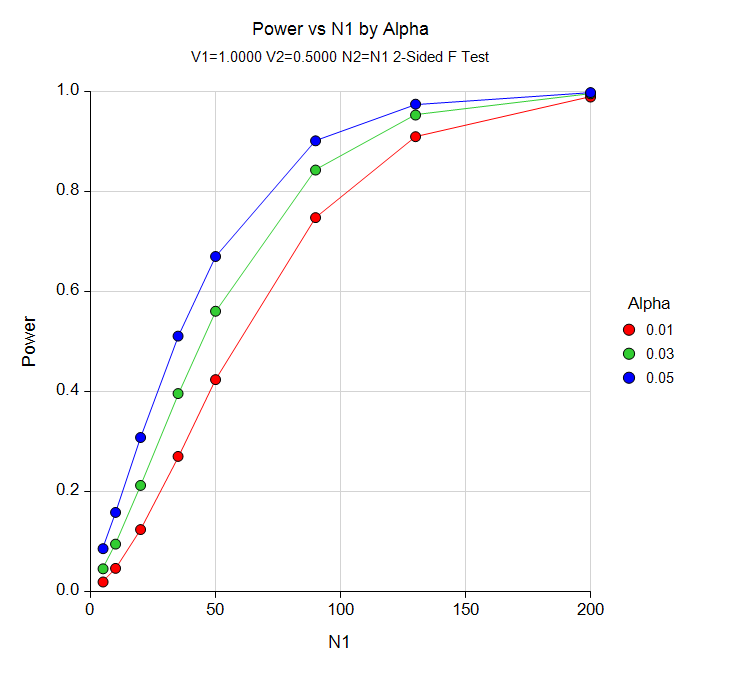
For the variance procedures in PASS, the user may choose to solve for sample size, power, or the variance value(s). In the case of confidence intervals, you can solve for sample size or the distance to the confidence limit. In a typical variance procedure where the goal is to estimate the sample size, the user enters power, alpha, and values for the variance(s). The procedure is run and the output shows a summary of the entries as well as the sample size estimate(s). A summary statement is given, as well as references to the articles from which the formulas for the result were obtained. For many of the parameters (e.g., power, alpha, sample size, confidence level, variance, standard deviation, etc.), multiple values may be entered in a single run. When this is done, estimates are made for every combination of entered values. A numeric summary of these results is produced along with easy-to-read sample size or power curve graphs.
Technical Details
This page provides a brief description of the tools that are available in PASS for power and sample size analysis for variances and standard deviation. If you would like to examine the formulas and technical details relating to a specific PASS procedure, we recommend you
download and install the free trial of the software, open the desired variances procedure, and click on the help button in the top right corner to view the complete documentation. There you will find summaries, formulas, references, discussions, technical details, examples, and validation against published articles for the procedure.
An Example Setup and Output
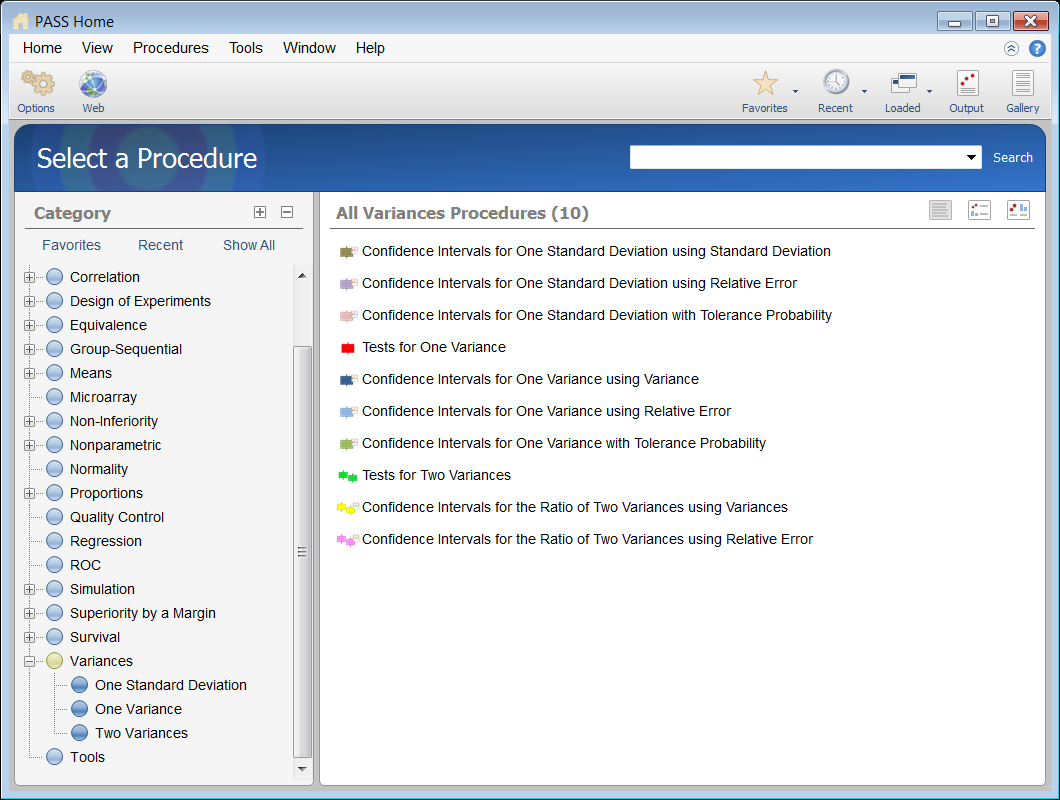
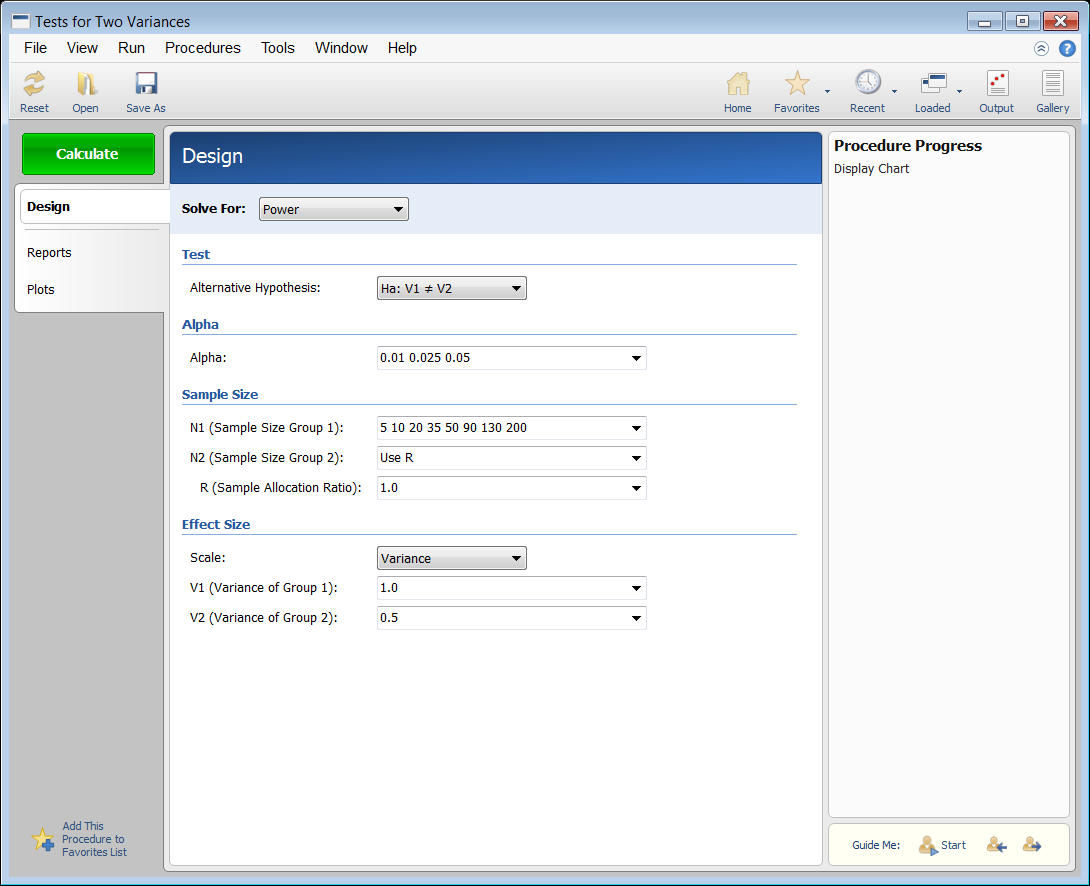
When the PASS software is first opened, the user is presented with the PASS Home window. From this window the desired procedure is selected from the menus, the category tree on the left, or with a procedure search. The procedure opens and the desired entries are made. When you click the Calculate button the results are produced. You can easily navigate to any part of the output with the navigation pane on the left.
PASS Home Window
Procedure Window for Testing Two Correlations
PASS Output Window

Sample Size for Tests for One Variance
Occasionally, researchers are interested in the estimation of the variance (or standard deviation) rather than the mean. The Tests for One Variance procedure in PASS calculates the sample size and performs power analysis for testing the null hypothesis H
0:
σ2 = σ02 versus the alternatives H
1:
σ2 <
σ02, H1: σ2 > σ02, or H
1:
σ2 ≠
σ02, where
σ2 is the variance from a normally distributed variable,
X.
Sample Size for Tests for Two Variances
The Tests for Two Variances procedure in PASS calculates the sample size and performs power analysis for testing the null hypothesis H
0:
σ12 = σ22 versus the alternatives H
1:
σ12 <
σ22, H1: σ12 > σ22, or H
1:
σ12 ≠
σ22, where
σ12 and
σ22 are variances from two normally distributed variables,
X1 and
X2.
In PASS, there are many procedures covering different variance comparison scenarios, including equivalence tests, non-inferiority tests, superiority by a margin tests, 2x2M replicated cross-over designs, total variances in a replicated design, and between variances.
There are also many sample size procedures for testing the ratio of two variances, including cases for within-subject variances, 2x2M cross-over designs, equivalence tests, non-inferiority tests, superiority by a margin tests, and replicated designs.
Sample Size for Confidence Intervals for One Variance
The Confidence Intervals for One Variance procedures in PASS calculate the sample size necessary to achieve a specified interval width or distance from the variance to the confidence limit at a stated confidence level for a confidence interval about the variance when the underlying data distribution is normal. The inputs can be specified using variances, relative error, or tolerance probability.
The Confidence Intervals for One Variance using Variance procedure assumes that the variance of the future sample will be the same as the variance that is specified. If the variance to be used in the procedure is estimated from a previous sample or represents the population variance, the Confidence Intervals for One Variance with Tolerance Probability procedure should be considered since it controls the probability that the width or the distance from the variance to the confidence limits will be less than or equal to the value specified. The Confidence Intervals for One Variance using Relative Error procedure controls the width or distance from the variance to the limits by controlling the width or distance as a percent of the true variance.
Sample Size for Confidence Intervals for the Ratio of Two Variances
The Confidence Intervals for the Ratio of Two Variances procedures in PASS calculate the group sample sizes necessary to achieve a specified interval width or distance from the variance ratio to the confidence limit at a stated confidence level for a confidence interval about the variance ratio when the underlying data distribution is normal. The inputs can be specified using variances or relative error.
The Confidence Intervals for the Ratio of Two Variances using Variances procedure assumes that the variances of the future samples will be the same as the variances that are specified. The Confidence Intervals for the Ratio of Two Variances using Relative Error controls the width or distance from the variance ratio to the limits by controlling the width or distance as a percent of the true variance ratio.
Sample Size for Confidence Intervals for One Standard Deviation
The Confidence Intervals for One Standard Deviation procedures in PASS calculate the group sample sizes necessary to achieve a specified interval width or distance from the variance ratio to the confidence limit at a stated confidence level for a confidence interval about the variance ratio when the underlying data distribution is normal. The inputs can be specified using variances, relative error, or tolerance probability.
The Confidence Intervals for One Standard Deviation using Standard Deviation procedure assumes that the standard deviation of the future sample will be the same as the standard deviation that is specified. If the standard deviation to be used in the procedure is estimated from a previous sample or represents the population standard deviation, the Confidence Intervals for One Standard Deviation with Tolerance Probability procedure should be considered since it controls the probability that the width or the distance from the standard deviation to the confidence limits will be less than or equal to the value specified. The Confidence Intervals for One Standard Deviation using Relative Error procedure controls the width or distance from the standard deviation to the limits by controlling the width or distance as a percent of the true standard deviation.




