Operations Research in NCSS
NCSS includes a wide range of tools for application in operations research. Use the links below to jump to the operations research topic you would like to examine. To see how these tools can benefit you, we recommend you download and install the free trial of NCSS. Jump to:- Introduction
- Technical Details
- Linear Programming with Bounds
- Linear Programming with Tableau
- Mixed Integer Programming
- Quadratic Programming
- Assignment
- Maximum Flow
- Minimum Cost Capacitated Flow
- Minimum Spanning Tree
- Shortest Route
- Transportation
- Transshipment
Introduction
Operations research uses various optimization algorithms to help make decisions related to highly complex problems. Linear Programming (LP) and Mixed Integer Programming (MIP) are often used to solve these highly complex decision-making problems. The operations research procedures available in the NCSS are described below.Technical Details
This page is designed to give a general overview of the capabilities of NCSS for operations research. If you would like to examine the formulas and technical details relating to a specific NCSS procedure, click on the corresponding '[Documentation PDF]' link under each heading to load the complete procedure documentation. There you will find formulas, references, discussions, and examples or tutorials describing the procedure in detail.Linear Programming with Bounds or Tableau
[Documentation PDF (with Bounds)][Documentation PDF (with Tableau)]
Linear Programming (LP) maximizes (or minimizes) a linear objective function subject to one or more constraints. The technique finds broad use in operations research and is occasionally of use in statistical work. The mathematical representation of the linear programming (LP) problem is to maximize (or minimize) the objective function
z = CX
subject to m constraintsAX ≤ b, X ≥ 0
The values in the X vector are called decision variables (the unknowns), and the values in the b vector are often called right-hand sides (RHS). NCSS solves a particular linear program using a revised dual simplex method available in the Extreme Optimization mathematical subroutine package.Sample Data
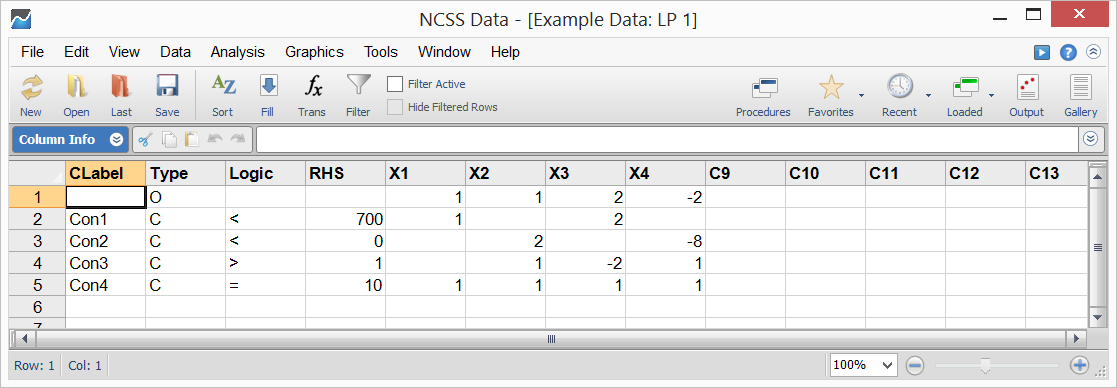
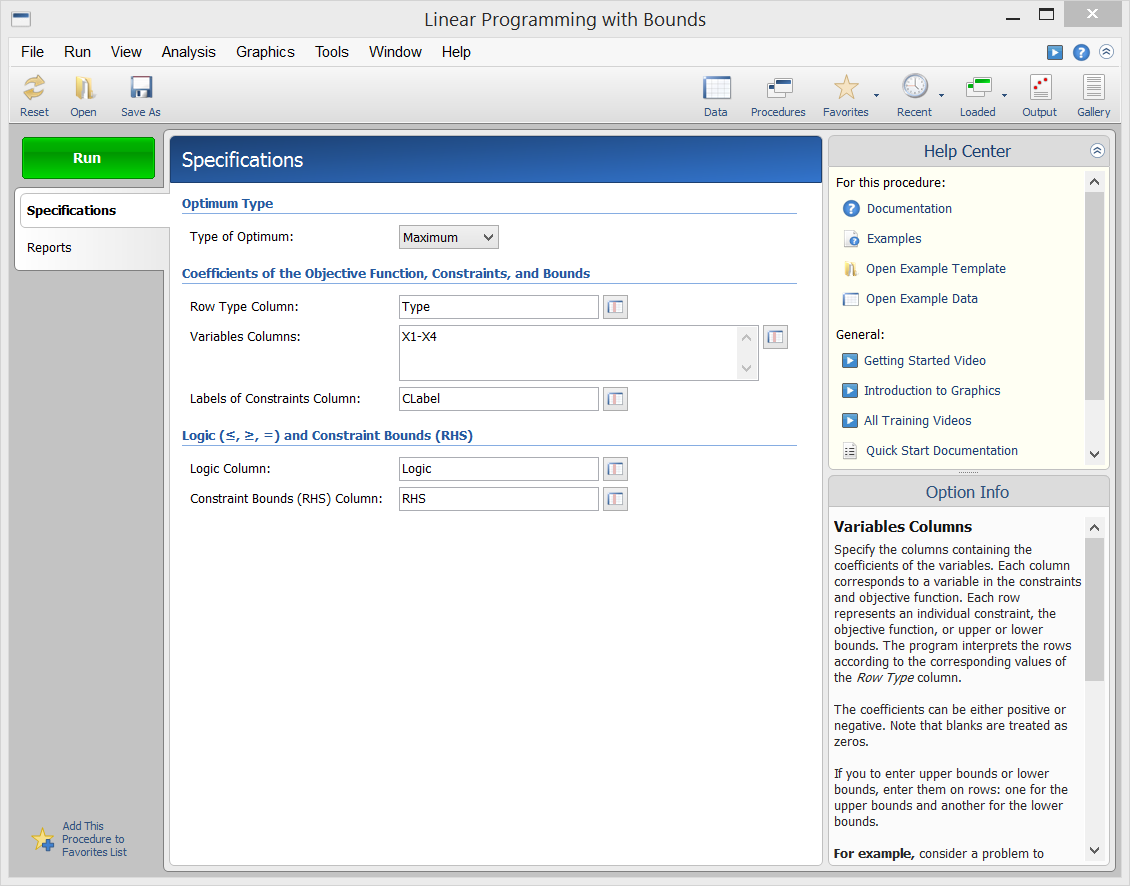
Procedure Input
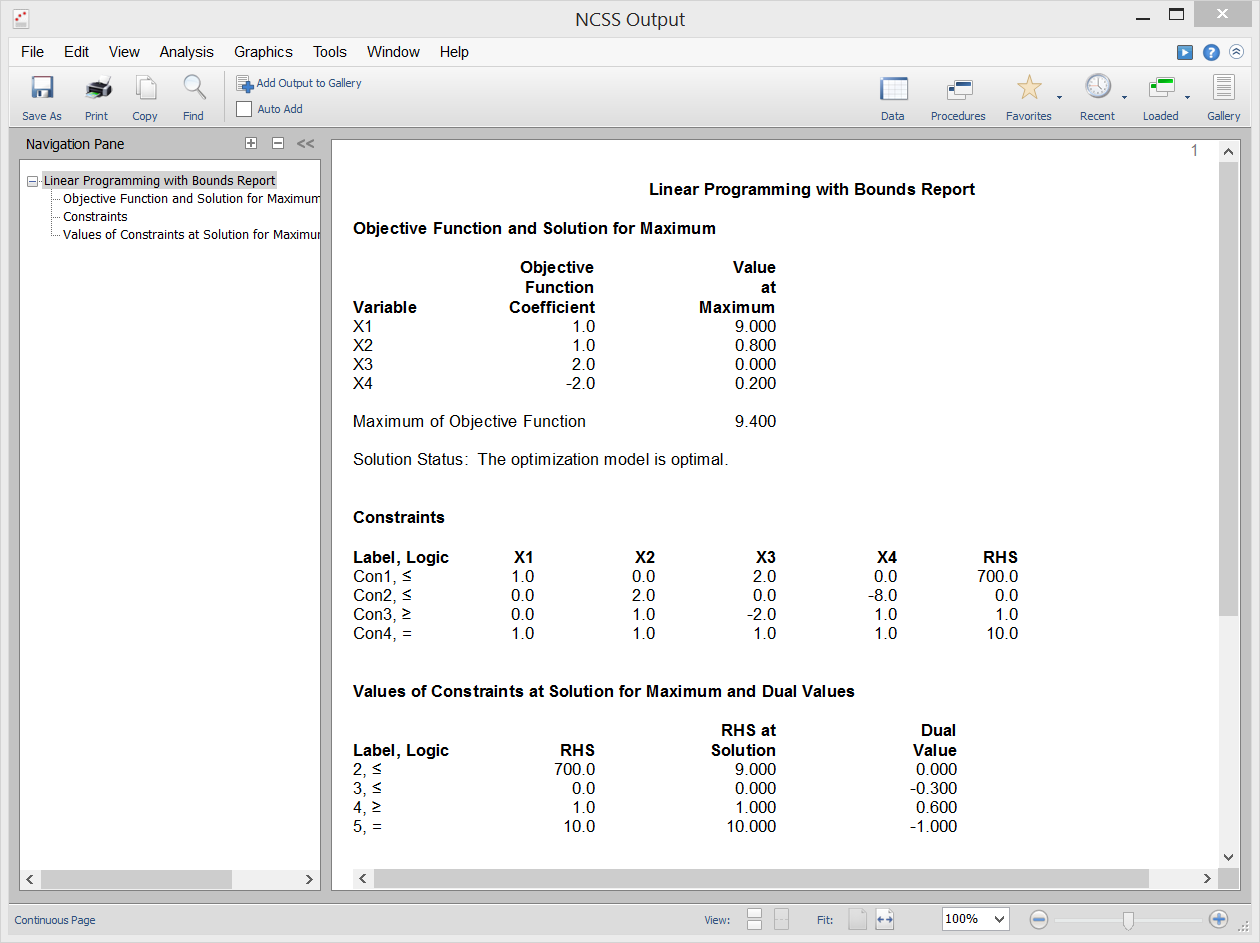
Sample Output
Mixed Integer Programming
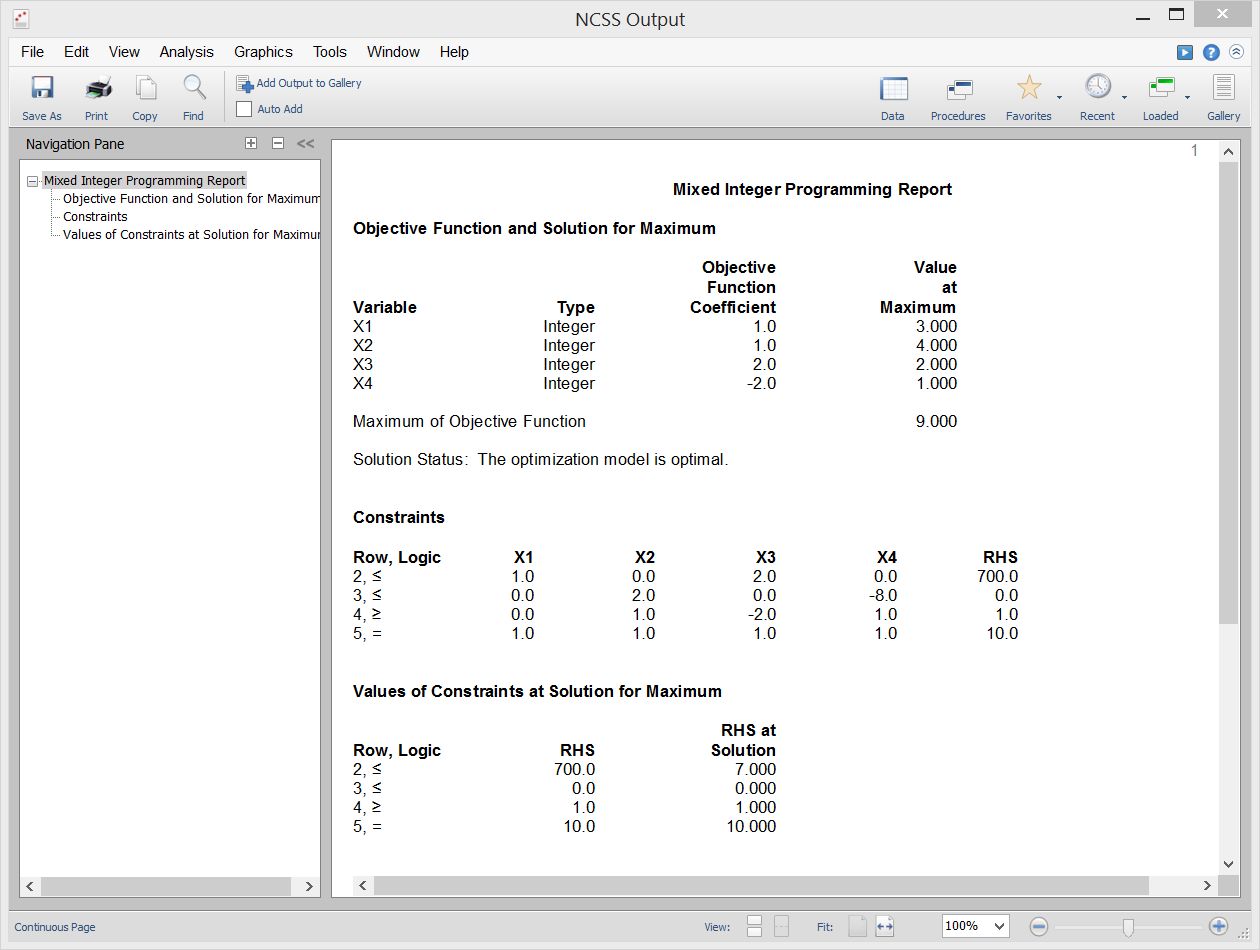
[Documentation PDF]Linear programming maximizes (or minimizes) a linear objective function subject to one or more constraints. Mixed Integer Programming (MIP) adds one additional condition that at least one of the variables can only take on integer values. The technique finds broad use in operations research. NCSS solves a particular mixed integer programming problem using the branch and bound algorithm available in the Extreme Optimization mathematical subroutine package.
Sample Output
Quadratic Programming
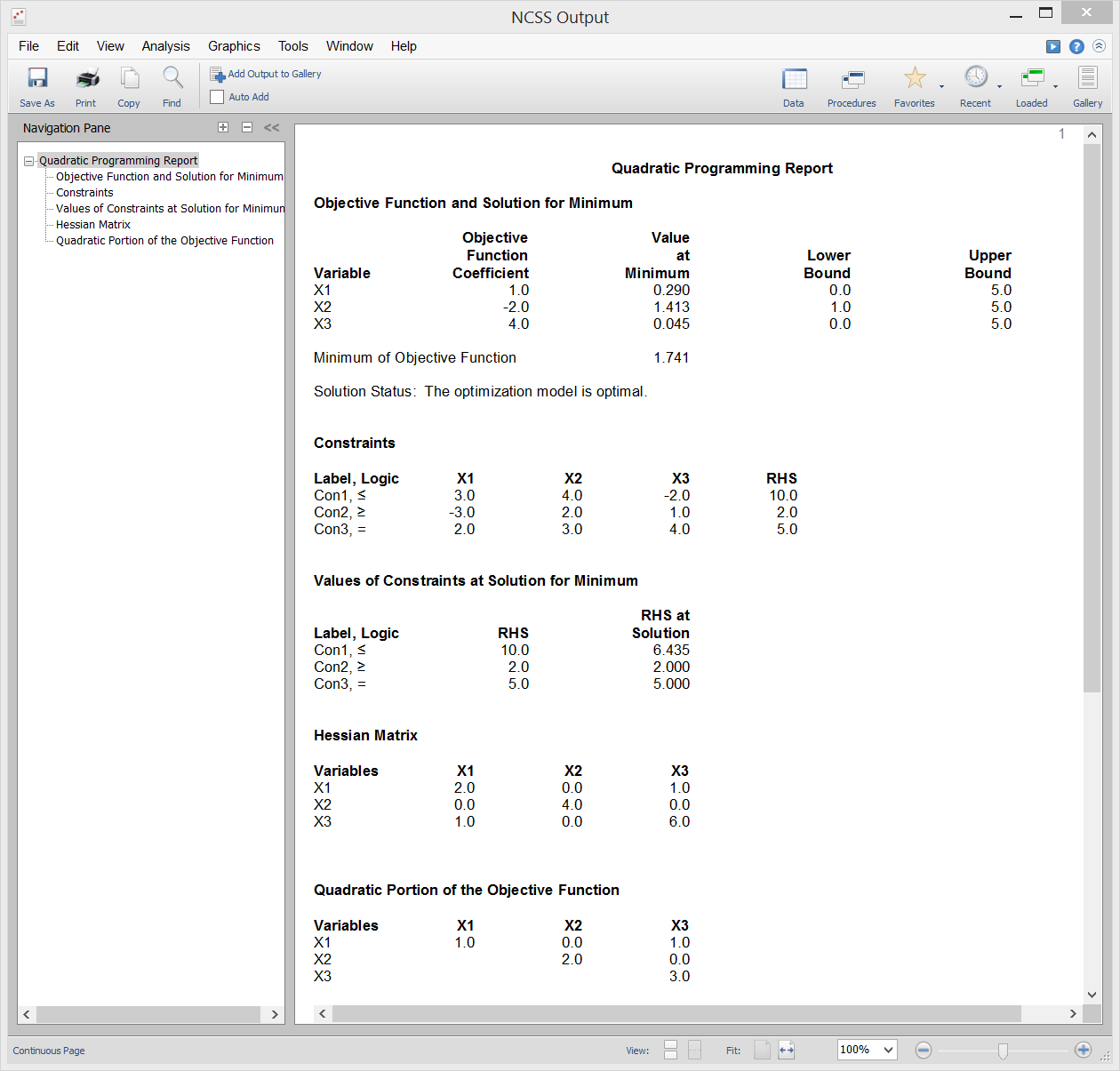
[Documentation PDF]Quadratic Programming maximizes (or minimizes) a quadratic objective function subject to one or more constraints. The technique finds broad use in operations research and is occasionally of use in statistical work. The mathematical representation of the quadratic programming (QP) problem is to maximize the objective function
z = CX + (1/2)X'HX or z = CX + X'DX
subject to m constraintsAX ≤ b, X ≥ 0
The values in the X vector are called decision variables (the unknowns), and the values in the b vector are often called right-hand sides (RHS). NCSS solves a particular quadratic program using a primal active set method available in the Extreme Optimization mathematical subroutine package.Sample Output
Assignment
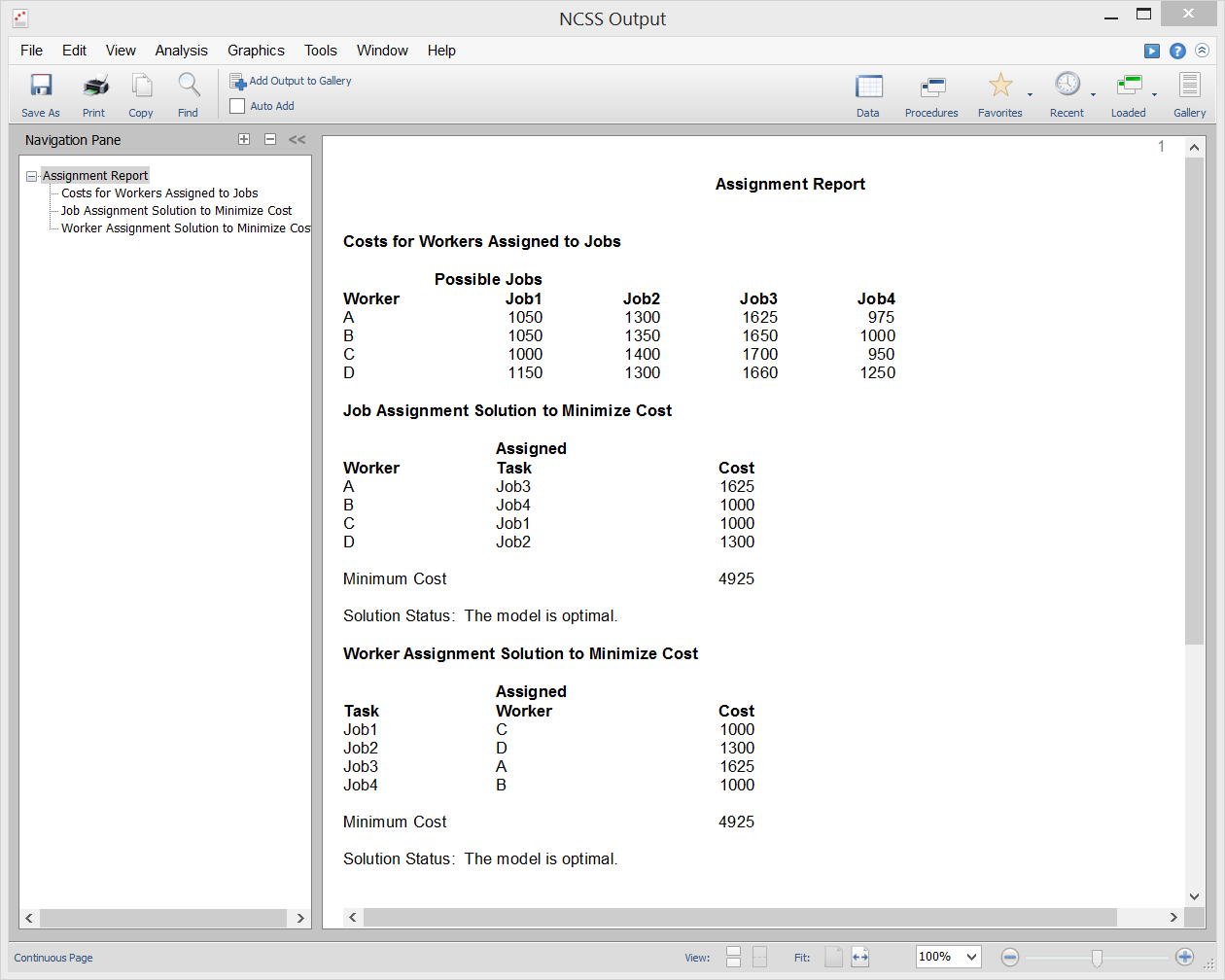
[Documentation PDF]The object of the Assignment algorithm is to assign n objects (workers, machines, etc.) to the same number of jobs (tasks) in such a way that will minimize the total cost. The problem assumes that only one task is assigned to each object. NCSS solves the problem using the mixed integer programming algorithm available in the Extreme Optimization mathematical subroutine package.
Sample Output
Maximum Flow
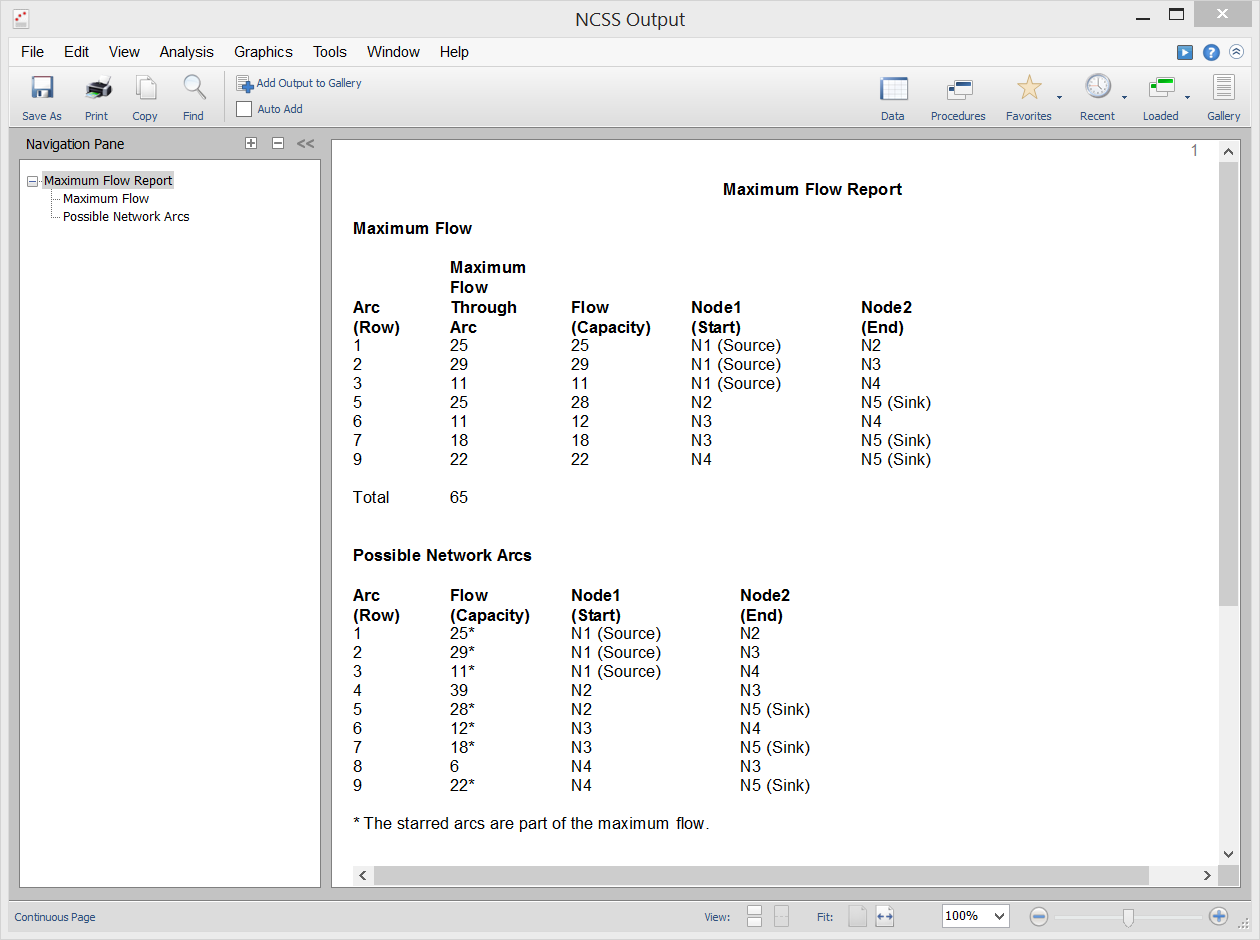
[Documentation PDF]Given a directed network defined by nodes, arcs, and flow capacities, this procedure finds the maximum flow that can occur between a source node and a sink node. An example of this is the flow of oil through a pipeline with several junctions. NCSS uses the linear programming approach to solve the problem as outlined in Taha (2011) and Hillier and Lieberman (2015).
Sample Output
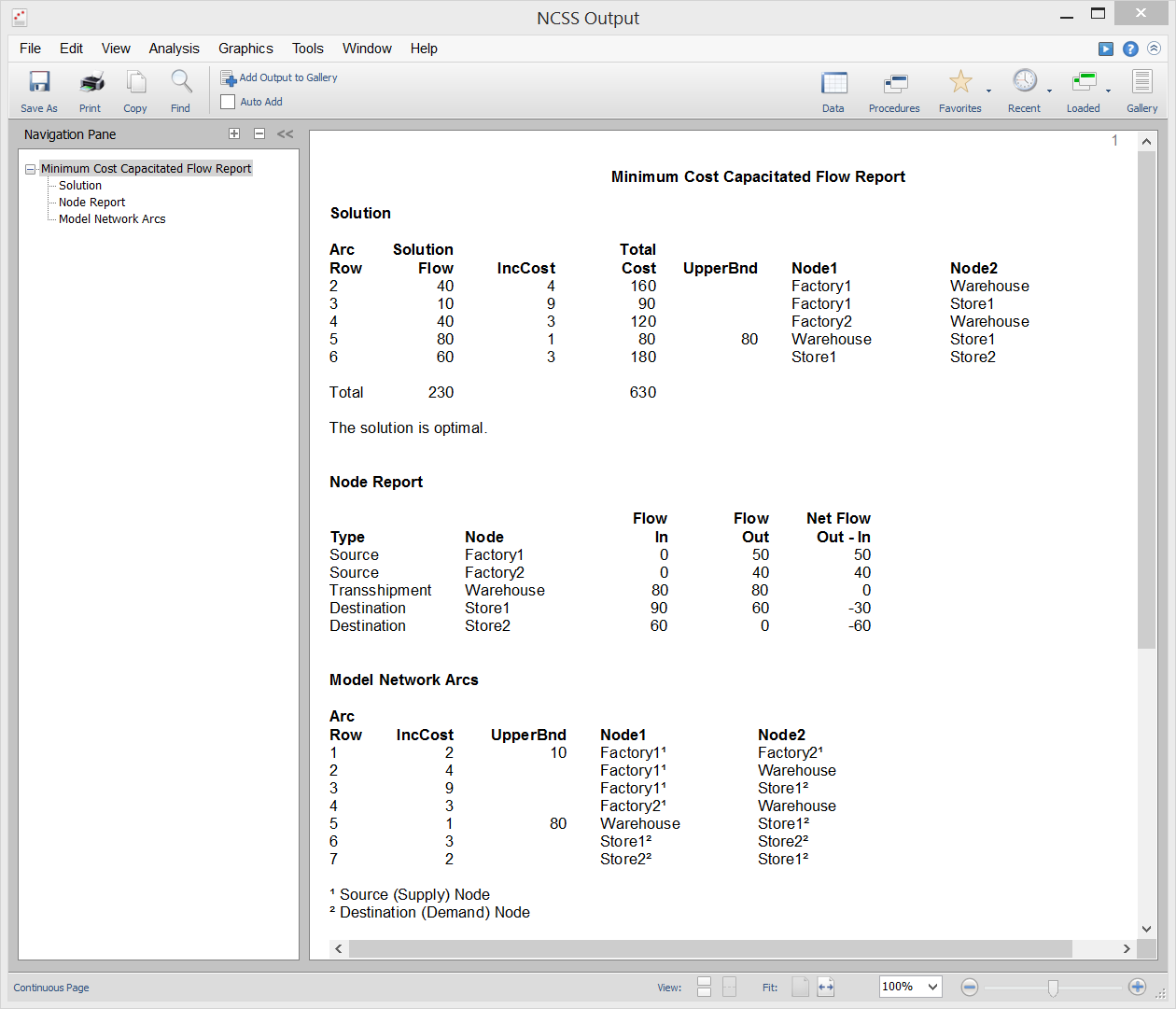
Minimum Cost Capacitated Flow
[Documentation PDF]The Minimum Cost Capacitated Flow model is prominent among network flow models because so many other network models are special cases. The maximum flow, shortest-path, transportation, transshipment, and assignment models are all special cases of this model. NCSS uses the linear programming approach to solve the problem as outlined in Hillier and Lieberman (2015).
Sample Output
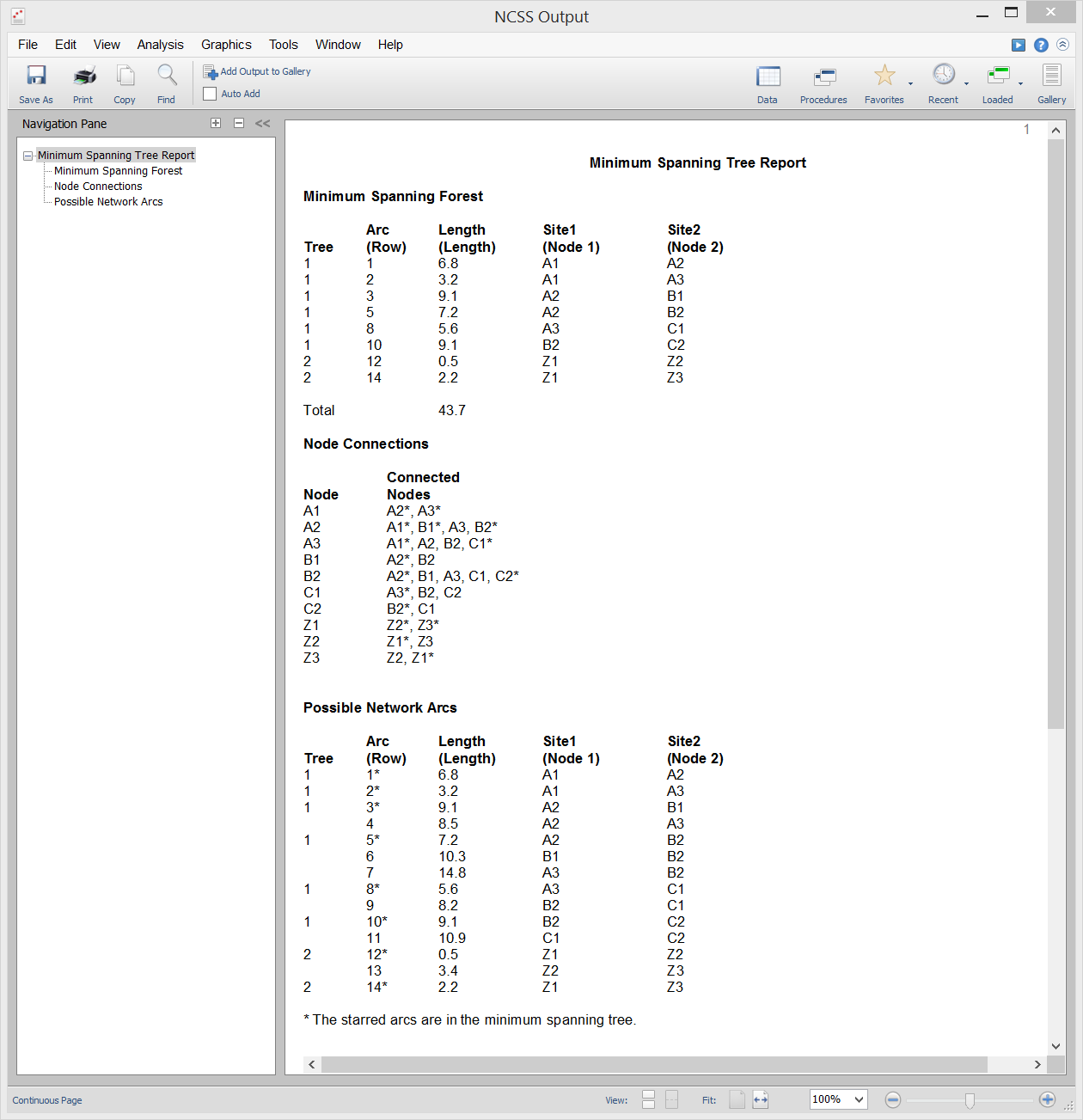
Minimum Spanning Tree
[Documentation PDF]A Minimum Spanning Tree links all nodes (points or vertices) of a network with the minimum length among all the arcs. This procedure finds the minimum spanning tree of a network using a greedy algorithm. If the network is not connected, the solution, called a minimum spanning forest, is a combination of minimum spanning trees formed on the connected subsets. The algorithm can be used in applications such as transportation networks, computer networks, and water networks where a tree connecting all nodes must have minimum length. The algorithm proceeds as follows:
- 1. Start with any node.
- 2. Connect this node to its nearest neighbor using any of the available branches.
- 3. Find the unconnected node that is closest any of the connected nodes. Connect these nodes.
- 4. Repeat steps 2 and 3 until all nodes have been connected.
Sample Output
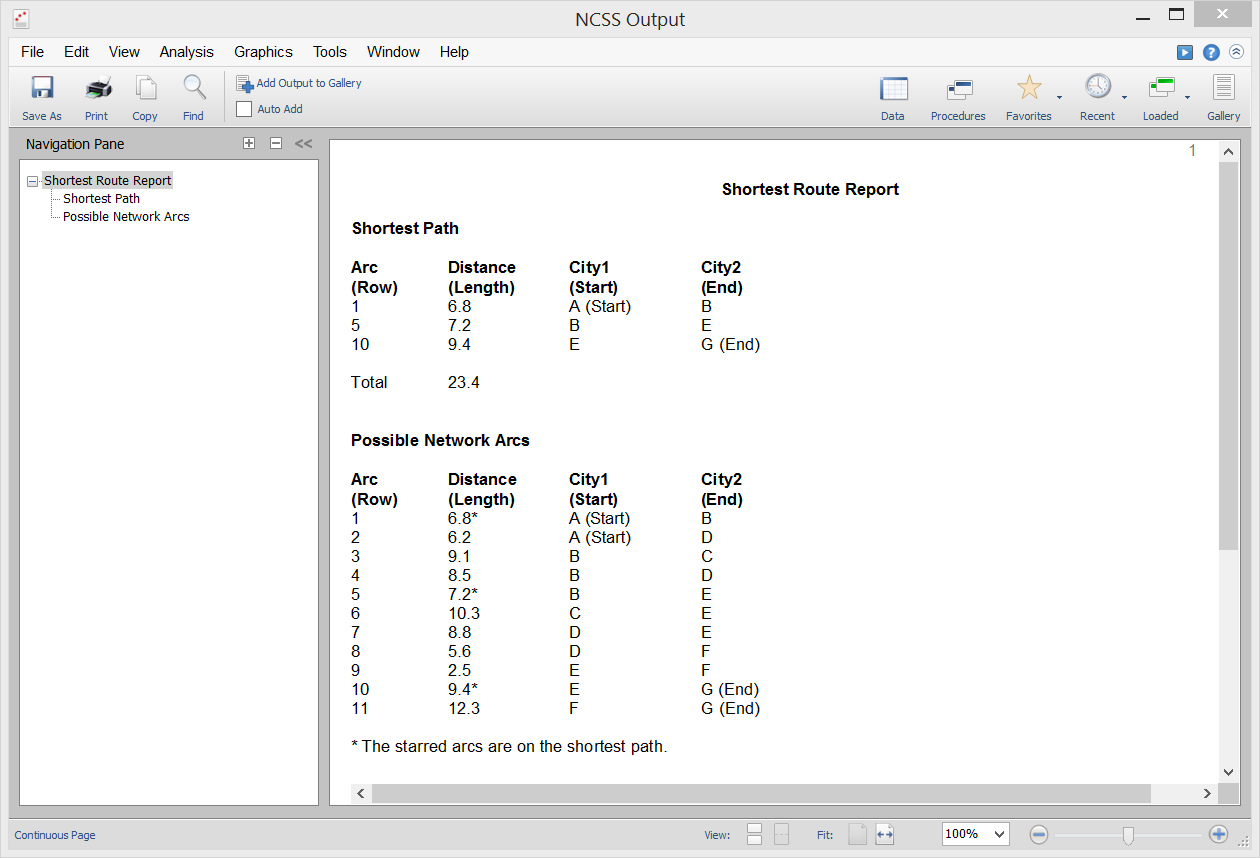
Shortest Route
[Documentation PDF]Given a directed network defined by nodes and arcs, this procedure finds the shortest route between two specified nodes. One example of the need for such an algorithm is to be used in a GPS device to find the shortest route between two locations. NCSS uses the linear programming approach to solve the problem as outlined in Taha (2011).
Sample Output
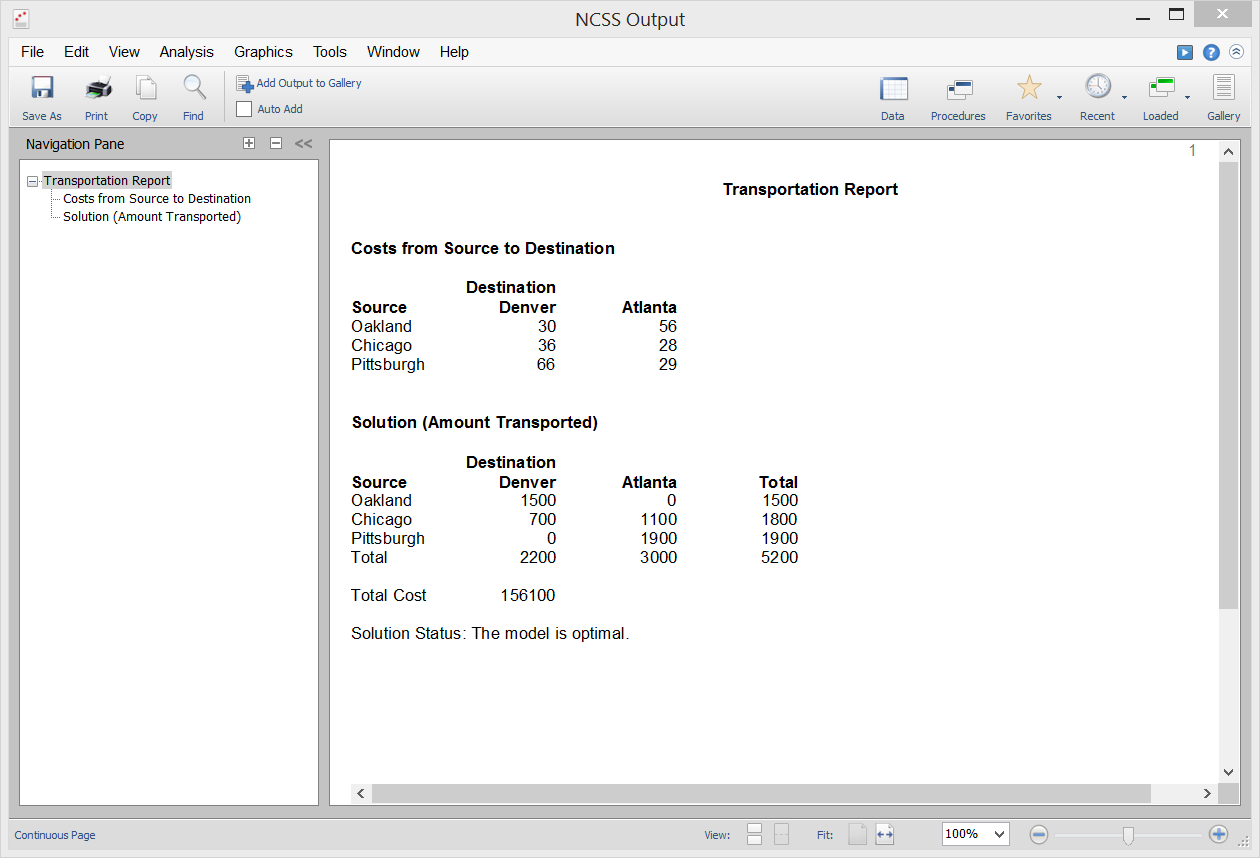
Transportation
[Documentation PDF]The object of the Transportation algorithm is to find the amounts shipped from m sources to n destinations that will minimize the total cost of distribution while meeting the demands at each destination and staying within the amount that can be supplied from each source. The problem assumes that only whole units can be shipped. NCSS solves the problem using the Mixed Integer Programming algorithm available in the Extreme Optimization mathematical subroutine package.
Sample Output
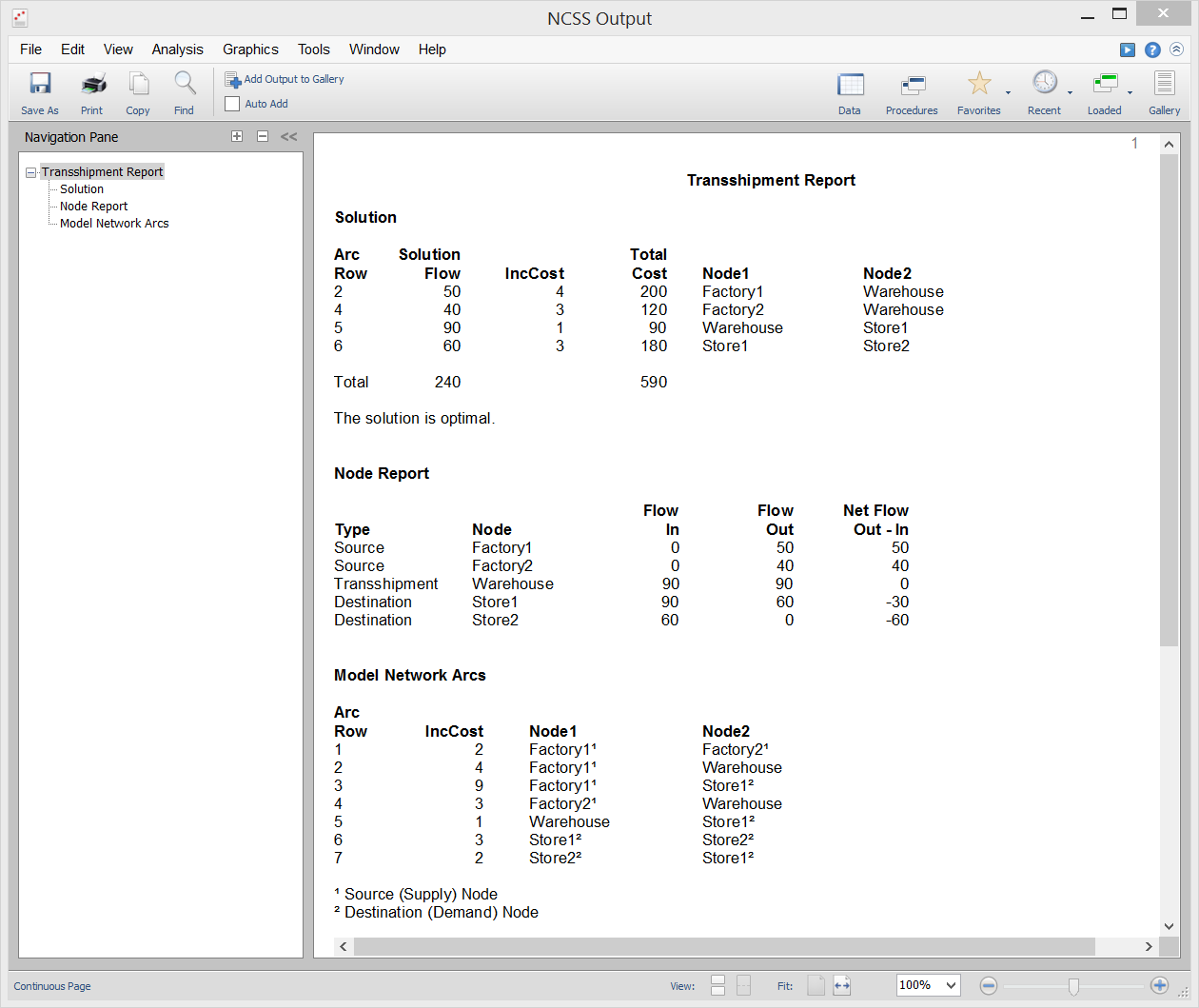
Transshipment
[Documentation PDF]The Transshipment model is a special case of the minimum cost capacitated flow model in which there are no capacities or minimums on the arc flows. The transshipment model is similar to a transportation model, except that it allows the more realistic assumption that all nodes can transfer to and from all other nodes, no matter what their node type. Hence, it allows product to be shipped between sources and between destinations, an ability that is missing in the transportation model. NCSS uses the linear programming approach to solve the problem as outlined in Hillier and Lieberman (2015).
Sample Output